
分析 (1)设y关于x的函数解析式为y=$\frac{k}{{x}^{2}}$,将点(2,20)代入其中得出关于k的一元一次方程,解方程即可得出结论;
(2)将x=-1代入(1)得出的函数解析式中,求出y值即可.
解答 解:(1)设y关于x的函数解析式为y=$\frac{k}{{x}^{2}}$,
由已知,得20=$\frac{k}{{2}^{2}}$,解得:k=80.
∴y关于x的函数解析式为y=$\frac{80}{{x}^{2}}$(x≠0).
(2)将x=-1代入y=$\frac{80}{{x}^{2}}$中,
y=$\frac{80}{(-1)^{2}}$=80.
答:当x=-1时,y的值为80.
点评 本题考查了待定系数法求反比例函数解析式,解题的关键是:(1)将点的坐标代入函数解析式中得出关于k的一元一次方程;(2)代入x=-1求出y值.本题属于基础题,难度不大,解决该题型题目时,将点的坐标代入函数解析式中得出方程(或方程组)是关键.


科目:初中数学 来源: 题型:选择题
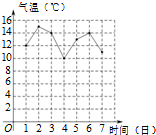 右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )
右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )| A. | 13,13 | B. | 14,14 | C. | 13,14 | D. | 14,13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
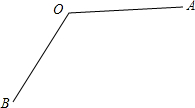 (1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);
(1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
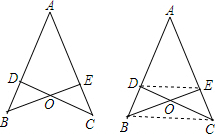 如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com