练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．如图，AB∥CD，AE交DE于点C，DE⊥AE，垂足为E，∠A=41°，求∠D的度数．

    分析 首先根据平行线的性质求得∠ECD的度数，然后在直角△ECD中，利用三角形内角和定理求解．

    解答 解：∵AB∥CD，
    ∴∠ECD=∠A=41°，
    又∵DE⊥AE，
    ∴直角△ECD中，∠D=90°-∠ECD=90°-41°=49°．

    点评 本题考查了平行线的性质以及三角形内角和定理，正确理解定理是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．如图是由六块积木搭成，这几块积木都是相同的正方体，请画出这个图形的三视图：
    从正面看           从左面看            从上面看．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

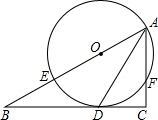    12．如图，在Rt△ABC中，∠C=90°，AC=12，BC=16，∠BAC的平分线交BC于D，经过A、D的⊙O交AB于E，并且点O在AB上
    （1）求证：BC是⊙O的切线；
    （2）求CD的长及⊙O的半径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．实数m，n在数轴上对应的点的位置如图所示，则$\sqrt{（m+n）^{2}}$-$\sqrt{{m}^{2}-2mn+{n}^{2}}$等于（　　）
    A．0B．2mC．2nD．2m+2n

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，在△ABC中，∠A=40°，∠B=78°，CD是∠ACB的角平分线，点E是CD上的点，EF⊥AB，垂足为F，求∠DEF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．在某小区花园中有x棵月季花，茶花的数量比月季花的棵数的3倍多7棵，则茶花的棵树是（　　）
    A．3x-7B．3x+7C．7x-3D．7x+3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

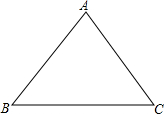    13．请思考如何利用位似变换的思想，在如图的三角形中作一个等边三角形，使它的三个顶点分别在已知三角形的边上，并且等边三角形的一边与BC平行，即：已知△ABC，求作等边△DEF，使它的三个顶点分别在△ABC的边上，且EF∥BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，⊙O内两条弦AB，CD相交于点E，已知AE=3cm，EB=8cm，CE=4cm，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

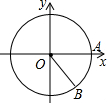    11．如图，以原点为圆心，2为半径的⊙O与正半轴交于点A，在⊙O上且在x轴的下方有一点B，∠AOB=45°，则点B的坐标为（$\sqrt{2}$，$-\sqrt{2}$）．

    查看答案和解析>>

    同步练习册答案