
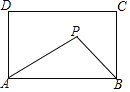
【题目】如图,在矩形ABCD中,AB=10,AD=6,动点P满足S△PAB=![]() S矩形ABCD,则△PAB周长的最小值_____
S矩形ABCD,则△PAB周长的最小值_____
【答案】10+2![]() .
.
【解析】
首先由S△PAB=![]() S矩形ABCD,得到动点P在与AB平行且与AB的距离是2的直线l上,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离,然后在Rt△ABE中,由勾股定理可求得BE的值,继而求得答案.
S矩形ABCD,得到动点P在与AB平行且与AB的距离是2的直线l上,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离,然后在Rt△ABE中,由勾股定理可求得BE的值,继而求得答案.
设△ABP中AB边上的高是h.
∵S△PAB=![]() S矩形ABCD,
S矩形ABCD,
∴![]() ABh=
ABh=![]() ABAD,
ABAD,
∴h=![]() AD=4,
AD=4,
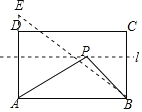
∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.
在Rt△ABE中,∵AB=10,AE=4+4=8,
∴BE=![]() ,
,
即PA+PB的最小值为![]() .
.
∴△PAB周长的最小值=10+![]() ,
,
故答案为:10+![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,某单位要建一个面积为48 m2的小仓库,小仓库有一边靠墙(墙长10m),并在与墙平行的一边开一道宽1 m的门,现有能围成19 m的木板,求小仓库的长与宽?
(注意:仓库靠墙的那一边不能超过墙长).

查看答案和解析>>
科目:初中数学 来源: 题型:
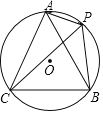
【题目】如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:PA+PB=PC;
(2)若BC=![]() ,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
,点P是劣弧AB上一动点(异于A、B),PA、PB是关于x的一元二次方程x2﹣mx+n=0的两根,求m的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
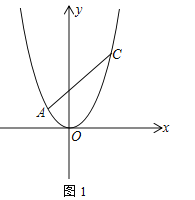
【题目】在平面直角坐标系中,抛物线![]() 经过点
经过点![]() ,
,![]() 、
、![]() ,
,![]() ,其中
,其中![]() 、
、![]() 是方程
是方程![]() 的两根,且
的两根,且![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线只有一个公共点
与抛物线只有一个公共点
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)求直线![]() 的解析式;
的解析式;
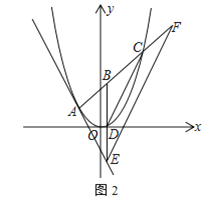
(3)如图2,点![]() 是线段
是线段![]() 上的动点,若过点
上的动点,若过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与抛物线相交于点
,与抛物线相交于点![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
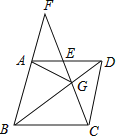
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
(1)求证:AG=CG;
(2)求证:AG2=GE·GF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,在AB的延长线上取一点E,使EF=ED,过点A作⊙O的切线交ED的延长线于点G.
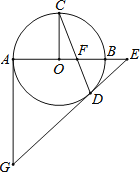
(1)求证:GE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径为3,求DE和AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中对 600 名毕业生中考体育测试坐位体前屈成绩进行整理,绘制成 如下不完整的统计图:
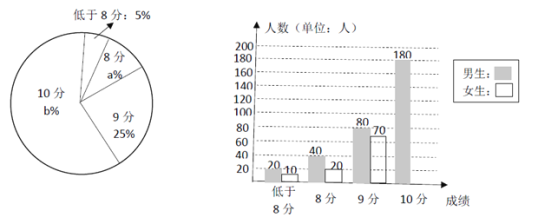
根据统计图,回答下列问题。
(1)请将条形统计图补充完整;
(2)扇形统计图中,b= ,得 8 分所对应扇形的圆心角度数为 ;
(3)在本次调查的学生中,随机抽取 1 名男生,他的成绩不低于 9 分的概率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com