
【题目】平行四边形 ABCD 中,两条邻边长分别为3和5,∠BAD与∠ABC的平分线交于点E,点F 是CD的中点,连接EF,则EF=________.
【答案】3.5或0.5
【解析】
分两种情况讨论:①当AB=3,BC=5时,延长AE交BC于M,由平行线的性质和角平分线的定义可推出∠BAM=∠AMB,得到AB=BM=3,求出CM=2,再证明∠AEB=90°,根据等腰三角形三线合一得到E为AM的中点,所以EF为梯形ADCM的中位线,根据中位线的性质可求EF;②当AB=5,BC=3时,延长AE交BC的延长线于M,连接DM,延长EF与DM交于G,同理可证AE=EM,CM=2,再利用三角形中位线的性质可求出EF.
分两种情况:
①如图1,当AB=3,BC=5时,延长AE交BC于M,
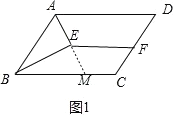
∵AD∥BC,
∴∠DAM=∠AMB
∵AM平分∠BAD,
∴∠DAM=∠BAM
∴∠BAM=∠AMB
∴AB=BM=3
∴CM=BC-BM=5-3=2
∵AD∥BC
∴∠DAB+∠ABC=180°
又∵AE平分∠BAD,BE平分∠ABC,
∴∠EAB+∠EBA=![]() ∠DAB+
∠DAB+![]() ∠ABC=90°,
∠ABC=90°,
∴∠AEB=90°
∴BE⊥AM,
∵BA=BM
∴AE=EM
∵DF=CF
∴EF为梯形ADCM的中位线
∴EF=![]()
②如图,当AB=5,BC=3时,
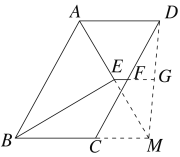
延长AE交BC的延长线于M,连接DM,延长EF与DM交于G,
同①可证:AE=EM,CM=BM-BC=AB-BC=2,
EG为△ADM的中位线,FG为△CDM的中位线,
∴EG=![]() AD=1.5,FG=
AD=1.5,FG=![]() CM=1,
CM=1,
∴EF=EG-FG=0.5
综上所述,EF的长为3.5或0.5
故答案为:3.5或0.5


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(0,4),线段
的坐标为(0,4),线段![]() 的位置如图所示,其中点
的位置如图所示,其中点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(3,
的坐标为(3,![]() ).
).

(1)将线段![]() 平移得到线段
平移得到线段![]() ,其中点
,其中点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①点![]() 平移到点
平移到点![]() 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点![]() 的坐标为 .
的坐标为 .
(2)在(1)的条件下,若点![]() 的坐标为(4,0),连接
的坐标为(4,0),连接![]() ,画出图形并求
,画出图形并求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰 Rt△ABC 中,∠ACB=90°,P 是射线CB上一点(在B点右侧),连接AP,延长PC至点Q,使得 CQ=CP,过点Q作QH⊥AP交PA延长线于点H,交BA延长线于点M,用等式表示线段MB与PQ之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
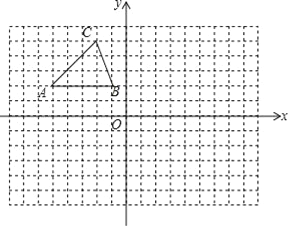
【题目】在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△A1B1C1关于y轴对称的△A2B2C2;
(3)若点P(a,b)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,写出P2的坐标为 ;
(4)试在y轴上找一点Q(在图中标出来),使得点Q到B2、C2两点的距离之和最小,并求出QB2+QC2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
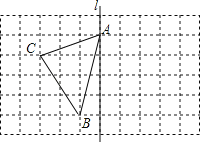
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)计算△ABC的面积;
(3)在直线l上找一点P,使PB+PC的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠A=40°,求∠DBC的度数.
(2)若△BCD的周长为16cm,△ABC的周长为26cm,求BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com