
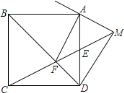
【题目】如图,边长为![]() 的正方形
的正方形![]() 中,
中,![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,则
,则![]() 的长为________.
的长为________.
【答案】![]()
【解析】
作MN⊥AD,先证明MA=ME,进而求出AN=NE=1,利用MN∥CD得:![]() ,
,
求出MN,在RT△MND中利用勾股定理即可求出DM.
作MN⊥AD垂足为N.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABF=∠CBF,BC∥AD,∠BAD=∠CDA=90°,
∵BF=BF,
∴△BFA≌△BFC,
∴∠BAF=∠BCF=∠CED=∠AEM,
∵∠MAF=∠BAD=90°,
∴∠BAF=∠MAE,
∴∠MAE=∠AEM,
∴MA=ME
∵AE=ED=![]() AD=2,
AD=2,
∴AN=NE=![]() AE=1,
AE=1,
∵∠MNE=∠CDE=90°,
∴MN∥CD,
∴△MNE∽△CDE,
∴![]() =
=![]() ,
,
∵CD=4,
∴MN=2,
在RT△MND中,∵MN=2,DN=3,
∴DM=![]() =
=![]() =
=![]() ,
,

故答案为:![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】平行四边形 ABCD 中,两条邻边长分别为3和5,∠BAD与∠ABC的平分线交于点E,点F 是CD的中点,连接EF,则EF=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
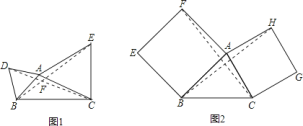
【题目】如图![]() ,以
,以![]() 边
边![]() 和
和![]() 为边作等边
为边作等边![]() 和
和![]() ,连接
,连接![]() ,
,![]() ,
,
![]() 判断
判断![]() 与
与![]() 的数量关系,并求
的数量关系,并求![]() 与
与![]() 的夹角
的夹角![]() 的度数;
的度数;
![]() 继续探索,如图
继续探索,如图![]() ,以
,以![]() 的
的![]() 和
和![]() 为边作正方形
为边作正方形![]() 和
和![]() ,连接
,连接![]() 、
、![]() ,判断
,判断![]() 和
和![]() 的数量关系,并求出此时
的数量关系,并求出此时![]() 与
与![]() 的夹角;
的夹角;
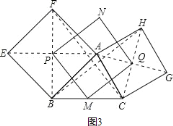
![]() 如图
如图![]() 中
中![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别是正方形的中心,顺次连接
分别是正方形的中心,顺次连接![]() ,判断四边形
,判断四边形![]() 的形状并证明.
的形状并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.(售价不低于进价).请根据小丽提供的信息,解答小华和小明提出的问题.

认真阅读上面三位同学的对话,请根据小丽提供的信息.
(1)解答小华的问题;
(2)解答小明的问题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com