
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() 的两个实数根的平方和为
的两个实数根的平方和为![]() ,那么
,那么![]() 的值是( )
的值是( )
A. 5 B. -1 C. 5或-1 D. -5或1
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】张三同学投掷一枚骰子两次,两次所投掷的点数分别用字母m、n表示
(1)求使关于x的方程x2﹣mx+2n=0有实数根的概率;
(2)求使关于x的方程mx2+nx+1=0有两个相等实根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
(1)如图①,在△ABC 中,∠B=30°,E 是 AB 边上的点,过点 E 作 EF⊥BC 于 F,则![]() 的值为 .
的值为 .
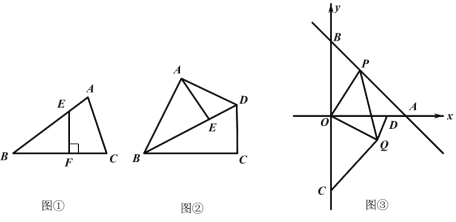
(2)如图②,在四边形 ABCD 中,AB=BC=6,∠ABC=60°,对角线 BD 平分∠ABC,点E 是对角线 BD 上一点,求 AE+ ![]() BE的最小值.
BE的最小值.
问题解决
(3)如图③,在平面直角坐标系中,直线 y -x 4 分别于 x 轴,y 轴交于点 A、B,点 P 为直线 AB 上的动点,以 OP 为边在其下方作等腰 Rt△OPQ 且∠POQ=90°.已知点C(0,-4),点 D(3,0)连接 CQ、DQ,那么DQ ![]() CQ是否存在最小值,若存在求出其最小值及此时点 P 的坐标,若不存在请说明理由.
CQ是否存在最小值,若存在求出其最小值及此时点 P 的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△ABlCl;
(2)点P在x轴上,且点P到点B与点C的距离之和最小,直接写出点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD的对角线交于点O,已知△OBC的周长为59厘米,且AD的长是28厘米,两对角线的差为14厘米,那么较长的一条对角线长是______厘米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形 ABCD 中,两条邻边长分别为3和5,∠BAD与∠ABC的平分线交于点E,点F 是CD的中点,连接EF,则EF=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.

(1)求正比例函数的表达式;
(2)在x轴上能否找到一点M,使△AOM是等腰三角形?若存在,求点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD,BE分别是∠BAC,∠ABC的角平分线.
(1)若∠C=70°,∠BAC=60°,则∠BED的度数是 ;若∠BED=50°,则∠C的度数是 .
(2)探究∠BED与∠C的数量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com