
【题目】如图,在△ABC中,AD,BE分别是∠BAC,∠ABC的角平分线.
(1)若∠C=70°,∠BAC=60°,则∠BED的度数是 ;若∠BED=50°,则∠C的度数是 .
(2)探究∠BED与∠C的数量关系,并证明你的结论.

【答案】(1)55°,80°;(2)∠BED=90°﹣![]() ∠C
∠C
【解析】
(1)根据三角形的内角和得到∠ABC=50°,根据角平分线的定义得到∠CAD=![]() ∠BAC=30°,∠DBE=
∠BAC=30°,∠DBE=![]() ∠ABC=25°,根据三角形的内角和即可得到结论;
∠ABC=25°,根据三角形的内角和即可得到结论;
(2)根据角平分线的定义和三角形的内角和即可得到结论.
(1)∵∠C=70°,∠BAC=60°,
∴∠ABC=50°,
∵AD,BE分别是∠BAC,∠ABC的角平分线,
∴∠CAD=![]() ∠BAC=30°,∠DBE=
∠BAC=30°,∠DBE=![]() ∠ABC=25°,
∠ABC=25°,
∵∠ADB=∠DAC+∠C=100°,
∴∠BED=180°﹣100°﹣25°=55°,
∵∠BED=50°,
∴∠ABE+∠BAE=50°,
∴∠ABC+∠BAC=2×50°=100°,
∴∠C=80°;
故答案为:55°,80°;
(2)∵AD,BE分别是∠BAC,∠ABC的角平分线,
∴∠ABE=![]() ∠ABC,∠BAE=
∠ABC,∠BAE=![]() ∠BAC,
∠BAC,
∵∠BED=∠ABE+∠BAE=![]() (∠ABC+∠BAC)=
(∠ABC+∠BAC)=![]() (180°﹣∠C)=90°﹣
(180°﹣∠C)=90°﹣![]() ∠C.
∠C.


科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
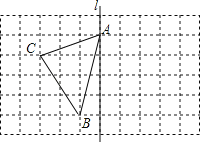
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)计算△ABC的面积;
(3)在直线l上找一点P,使PB+PC的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O为坐标原点,四边形OABC为长方形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动.
(1)当△ODP是等腰三角形时,请直接写出点P的坐标;
(2)求△ODP周长的最小值.(要有适当的图形和说明过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,CE⊥AD于点E,且CB=CE,点F为CD边上的一点,CB=CF,连接BF交CE于点G.
(1)若∠D=60°,CF=2![]() ,求CG的长度;
,求CG的长度;
(2)求证:AB=ED+CG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN. 求证:
(1)△APM是等腰三角形;
(2)PC=AN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠A=40°,求∠DBC的度数.
(2)若△BCD的周长为16cm,△ABC的周长为26cm,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,P是x轴上的一动点,连接CP.
(1)直接写出OC=___________;
(2)如图1,当CP与⊙A相切时,求PO的长;
(3)如图2,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问当PO为何值时,△OCQ是等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个文具店均出售钢笔和笔记本,其中每支钢笔定价10元,每本笔记本定价5元.两个文具店在开展促销活动中,各自提出优惠方案如下:
甲店:买一支钢笔送一本笔记本;
乙店:买钢笔或笔记本都按定价的80%付款.
现小明要购买钢笔30支,笔记本![]() 本(
本(![]() >30).
>30).
(1)试用含![]() 的代数式表示:
的代数式表示:
①小明到甲店购买所付款为 元;
②小明到乙店购买所付款为 元;
(2)当![]() 40时,你能帮小明设计一种最为省钱的购买方案吗?试写出你的购买方案,并说明理由.
40时,你能帮小明设计一种最为省钱的购买方案吗?试写出你的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com