
【题目】已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN. 求证:
(1)△APM是等腰三角形;
(2)PC=AN.

【答案】(1)见解析;(2)见解析
【解析】
(1)利用条件得到∠BAM=∠ANM=90°,∠PAQ=∠AMN即可解答.
(2)转换角度,利用角平分线性质解答.
(1)解:∵BA⊥AM,MN⊥AC,
∴∠BAM=∠ANM=90°,
∴∠PAQ+∠MAN=∠MAN+∠AMN=90°,
∴∠PAQ=∠AMN,
∵PQ⊥AB,MN⊥AC,
∴∠PQA=∠ANM=90°,
在△AQP和△MNA中,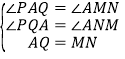
∴△AQP≌△MNA,
∴MA=AP,
∴△APM是等腰三角形.
(2)解:∵MA=AP,
∴∠AMP=∠APM,
∵∠APM=∠BPC,
∴∠AMP=∠BPC,
∵∠BPC+∠PBC=90°,∠AMB+∠ABM=180°-∠BAM=90°,
∴∠ABM=∠PBC,
∵PQ⊥AB,PC⊥BC,
∴PQ=PC(角平分线的性质),
由(1)可知AN=PQ,
∴PC=AN.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价2元收费;若每月用水量超过14吨,则超过部分每吨按市场价3.5元收费.小明家2月份用水20吨,交水费49元;3月份用水18吨,交水费42元.
(1)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(2)小明家5月份用水30吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.

(1)若∠DEC=25°,求∠B的度数;
(2)求证:直线AD是线段CE的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队要从小军和小勇两名队员中选派一人参加市篮球协会的投篮比赛,在最近的十次选拔测试中,他俩投篮十次的进球个数如下表所示:
小军 | 7 | 8 | 8 | 8 | 8 | 9 | 8 | 9 | 7 | 8 |
小勇 | 7 | 8 | 9 | 5 | 9 | 10 | 7 | 10 | 9 | 6 |
(l)请填写下表:
平均数 | 中位数 | 众数 | 极差 | 方差 | |
小军 | 8 | 8 | ______ | span>2 | ______ |
小勇 | ______ | ______ | 9 | _______ | 2.6 |
(2)历届比赛成绩表明,十次投进八球就很可能获奖但很难夺冠,十次投进九球就很可能夺冠,那么你认为想要获奖应该派谁参赛,想要夺冠应该派谁参赛?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=![]() x上,则点A2018的坐标为( )
x上,则点A2018的坐标为( )

A. (2018![]() ,2020) B. (2018
,2020) B. (2018![]() ,2018) C. (2020
,2018) C. (2020![]() ,2020) D. (2018,2020)
,2020) D. (2018,2020)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,4),B(﹣4,n)两点.
的图象交于A(2,4),B(﹣4,n)两点.
(1)分别求出一次函数与反比例函数的表达式;
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.
【1】求证:△ABE≌△CDA;
【2】若∠DAC=40°,求∠EAC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在四边形ABCD中,∠A=90°.若AB=4cm,AD=3cm,CD=12cm,BC=13cm,
(1)请说明BD⊥CD;
(2)求四边形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com