
 已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )
已知△ABC的三边长分别为2,3,4,M为三角形内一点,过点M作三边的平行线,交各边于D、E、F、P、Q(如图).如果DE=FG=PQ=x,则x=( )| A. | $\frac{18}{13}$ | B. | $\frac{20}{13}$ | C. | $\frac{22}{13}$ | D. | $\frac{24}{13}$ |
分析 首先证得四边形BDPM,四边形AFMQ,四边形CEMG均为平行四边形,利用平行线分线段成比例定理可得AD,AE,易得BD,PM,QM,利用平行四边形的性质可得PM,MG,由AA定理易得△QME∽△MPG,利用相似三角形的性质列方程,解得x.
解答 解:∵PQ∥AB,DE∥BC,FG∥AC,
∴四边形BDPM,四边形AFMQ,四边形CEMG均为平行四边形,
∵DE∥BC,
∴$\frac{DE}{BC}=\frac{AD}{AB}=\frac{AE}{AC}$,
∴$\frac{x}{4}=\frac{AD}{2}=\frac{AE}{3}$,
∴AD=$\frac{1}{2}x$,AE=$\frac{3}{4}x$,
∴BD=2-$\frac{1}{2}x$=PM,CE=3-$\frac{3}{4}x$=MG,
∴QM=x-PM=x-2$+\frac{1}{2}x$=$\frac{3}{2}x-2$,
FM=x-MG=x-3$+\frac{3}{4}x$=$\frac{7}{4}x$-3=AQ,
∴QE=$\frac{3}{4}x-\frac{7}{4}x+3$=3-x,
∵FG∥AC,DE∥BC,
∴∠QEM=∠MGP,∠MQE=∠PMG,
∴△QME∽△MPG,
∴$\frac{QM}{PM}=\frac{QE}{MG}$,
∴$\frac{\frac{3}{2}x-2}{2-\frac{1}{2}x}=\frac{3-x}{3-\frac{3}{4}x}$,
解得x=$\frac{24}{13}$.
故选D.
点评 本题主要考查了平行四边形的判定及性质定理和相似三角形的判定及性质定理,能够用x表示出其它边的长是解答此题的关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
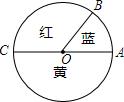 一个转盘的颜色如图所示,其中∠AOB=60°,∠BOC=120°,则转动转盘时,指针落在红色区域的概率是( )
一个转盘的颜色如图所示,其中∠AOB=60°,∠BOC=120°,则转动转盘时,指针落在红色区域的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正多边形都是中心对称图形 | |
| B. | 经过三角形重心的直线平分三角形的面积 | |
| C. | 在同圆中,相等的弦所对的圆周角相等 | |
| D. | 圆内接平行四边形一定是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
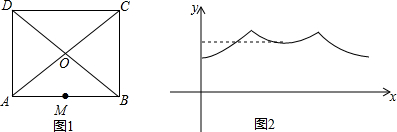
| A. | D→O→C | B. | A→D→C→B | C. | A→D→O→C→B | D. | O→D→C→O |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
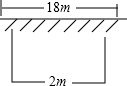 如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,
如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
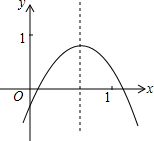 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是( )| A. | a>0 | B. | abc>0 | C. | a+b+c<0 | D. | b2-4ac<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com