
����Ŀ��ij�̳�����A��B��������С�ҵ磬A��ÿ̨����40Ԫ���ۼ�50Ԫ��B��ÿ̨����32Ԫ���ۼ�40Ԫ��4�·��۳�A��40̨��������������С�ҵ繲����������800Ԫ��
��1����4�·��۳�B��С�ҵ����ٶ���̨��
��2�����г����飬5�·�A���ۼ�ÿ����1Ԫ������������10̨��B���ۼ�ÿ����1Ԫ����������4�·���������Ļ���������15̨��Ϊ���������������ʵ�ݣ��̳��ƻ�5�·�A��B����С�ҵ綼������ͬ�۸���ϣ������������С�ҵ繲����965Ԫ����������С�ҵ綼Ӧ���Ͷ���Ԫ��
���𰸡���1��4�·��۳�B��С�ҵ�����50̨����2�������ͺŵ�С�ҵ綼����3Ԫ��
��������
��1����4�·��۳�B��С�ҵ�x̨�����ݡ�����������С�ҵ繲����������800Ԫ���г�����ʽ�����
��2���������ͺŵ�С�ҵ綼����yԪ�����ݡ����������ۼ۩����ۣ��������������г����̲����
�⣺��1����4�·��۳�B��С�ҵ�x̨��
�������⣬�ã�50��40����40+��40��32��x��800��
���x��50��
��4�·��۳�B��С�ҵ�����50̨��
��2���������ͺŵ�С�ҵ綼����yԪ���������⣬�ã�
![]()
��������![]() ��
��
���y1��3��y2��2.2��
Ϊ���������ߵõ������ʵ�ݣ�����y��3�������⣮
�������ͺŵ�С�ҵ綼����3Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��3��BC��2��EΪBC���е㣬AF��1����EFΪֱ���İ�Բ��DE���ڵ�G�����ӻ�![]() �ij�Ϊ_____��
�ij�Ϊ_____��
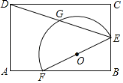
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У���![]() ΪԲ�ģ��ڵ�һ�����ڻ�Բ������˫���߽������㣬��
ΪԲ�ģ��ڵ�һ�����ڻ�Բ������˫���߽������㣬��![]() ��Բ����һ�����㣬����
��Բ����һ�����㣬����![]() ���ӳ�����������˫�����ڵ�
���ӳ�����������˫�����ڵ�![]() ����
����![]() �ᣬ
�ᣬ![]() �ᣬֻ�е�
�ᣬֻ�е�![]() ʱ��
ʱ��![]() ����
����![]() �İ뾶Ϊ_____________________��
�İ뾶Ϊ_____________________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬��y�ύ�ڵ�
��x�ύ��A��B���㣬��y�ύ�ڵ�![]() ���Ҵ������ߵĶ�������Ϊ
���Ҵ������ߵĶ�������Ϊ![]() ��
��
![]() ��������ߵĽ���ʽ��
��������ߵĽ���ʽ��
![]() ���DΪ��֪�����߶Գ����ϵ�����һ�㣬��
���DΪ��֪�����߶Գ����ϵ�����һ�㣬��![]() ��
��![]() ������ʱ�����D�����ꣻ
������ʱ�����D�����ꣻ
![]() ��P���߶�AM�ϣ���PC��y�ᴹֱʱ������P��x��Ĵ��ߣ�����ΪE����
��P���߶�AM�ϣ���PC��y�ᴹֱʱ������P��x��Ĵ��ߣ�����ΪE����![]() ��ֱ��CE���ۣ�ʹ��P�Ķ�Ӧ��
��ֱ��CE���ۣ�ʹ��P�Ķ�Ӧ��![]() ��P��E��C����ͬһƽ���ڣ��������
��P��E��C����ͬһƽ���ڣ��������![]() ���꣬���жϵ�
���꣬���жϵ�![]() �Ƿ��ڸ��������ϣ�
�Ƿ��ڸ��������ϣ�
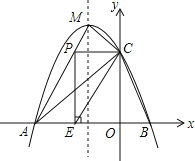
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ABC�У�AB��AC��2����ABC��30�㣬ADΪBC���ϵĸߣ�E��F�ֱ�ΪAB��AC���ϵĵ㣬����ABC�ֱ���DE��DF�۵���ʹ��B����DA���ӳ����ϵ�M������C���ڵ�N��������MN����MN��AC����AF�ij���_____��
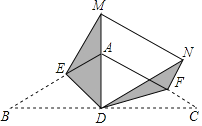
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ����������ϣ���
����������ϣ���![]() ��
��![]() ����������һ���㣬����
����������һ���㣬����![]() ����
����![]() Ϊ�߳�����
Ϊ�߳�����![]() ���Ҳ����ȱ�
���Ҳ����ȱ�![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() ��������Ϊ
��������Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ��________��
�ĺ�����ϵʽ��________��
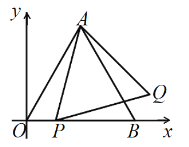
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]()
![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() ���ڵ�
���ڵ�![]() ���������ߵĶԳ��ᾭ����
���������ߵĶԳ��ᾭ����![]() ������
������![]() ��ֱ��
��ֱ��![]() ������������һ��
������������һ��![]() ����
����![]() �Ǹ���������һ�㣬����
�Ǹ���������һ�㣬����![]() ��
��![]() ��
��![]() ��
��![]() ��
��

��1����ֱ��![]() �������ߵĺ�������ʽ��
�������ߵĺ�������ʽ��
��2�����ʣ�![]() �����Ƿ����ijһ��
�����Ƿ����ijһ��![]() ��ʹ���Ե�
��ʹ���Ե�![]() ��
��![]() ��
��![]() �����
�����![]() ��
��![]() ���ƣ������ƣ��������ʱ��
���ƣ������ƣ��������ʱ��![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
��3������![]() ��ֱ��
��ֱ��![]() �Ϸ�����������һ���㣨�����
�Ϸ�����������һ���㣨�����![]() ��
��![]() �غϣ�����
�غϣ�����![]() ��
��![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊֱ����
Ϊֱ����![]() ����
����![]() ��ֱ��
��ֱ��![]() �����صõ��߶γ��ȵ����ֵ����_______����ֱ��д���𰸣�
�����صõ��߶γ��ȵ����ֵ����_______����ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ��
��![]() ��ֱ����
��ֱ����![]() ���ӳ�������һ��
���ӳ�������һ��![]() ��
��![]() ��
��![]() �����ߣ��е�Ϊ
�����ߣ��е�Ϊ![]() ������
������![]() ��
��![]() ������Ϊ
������Ϊ![]() ������
������![]() ��
��
��1����ͼ1����֤��![]() ��
��
��2����ͼ2��![]() ��
��![]() �ϵĵ㣬����
�ϵĵ㣬����![]() ��
��![]() ����
����![]() ��
��
��֤��![]() ��
��
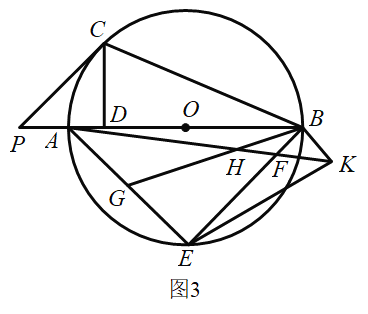
��3����ͼ3���ڣ�2���������£���![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() �ϣ�����
�ϣ�����![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ���ӳ�
���ӳ�![]() ����
����![]() ������
������![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����߶�
�����߶�![]() �ij���
�ij���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �ǡ�O��ֱ����
�ǡ�O��ֱ����![]() ����
����![]() �ڡ�O�İ뾶
�ڡ�O�İ뾶![]() ���˶���
���˶���![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() Ϊ��O�����ߣ��е�Ϊ
Ϊ��O�����ߣ��е�Ϊ![]() ��
��
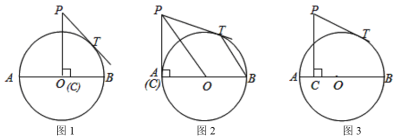
��1����ͼ1����![]() ���˶���
���˶���![]() ��ʱ����
��ʱ����![]() �ij���
�ij���
��2����ͼ2����![]() ���˶���
���˶���![]() ��ʱ������
��ʱ������![]() ��
��![]() ����֤��
����֤��![]() ��
��![]() ��
��
��3����ͼ3����![]() ��
��![]() ����y��x�Ľ���ʽ�����y����Сֵ��
����y��x�Ľ���ʽ�����y����Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com