
【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD.
(1)如图1,直接写出∠ABD的大小(用含α的式子表示);
(2)如图2,若∠BCE=150°,∠ABE=60°, ∠DEC=45°,求α的值;
(3)如图3,若∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明.

【答案】(1)30-![]() α;(2)α=30°(3)△ABE是等边三角形,理由见解析.
α;(2)α=30°(3)△ABE是等边三角形,理由见解析.
【解析】
(1)根据等腰三角形的性质求出∠ABC的度数,即可求出答案;
(2)连接AD,CD,由旋转的性质可证△BCD为等边三角形,根据SSS证明△ABD≌△ACD,可得∠BAD=∠CAD,∠ADB=∠ADC;根据AAS证明△ABD≌△EBC(AAS),可得∠EBC=∠ABD=30-![]() α;然后再证明△DEC为等腰直角三角形,得到DC=CE=BC,根据∠EBC=30-
α;然后再证明△DEC为等腰直角三角形,得到DC=CE=BC,根据∠EBC=30-![]() α=15可求出α的值;
α=15可求出α的值;
(3)由△ABD≌△EBC和∠ABE=60°,可证△ABE是等边三角形.
解:(1)∵AB=AC,∠A=α,
∴∠ABC=∠ACB=![]() (180-∠A)=90-
(180-∠A)=90-![]() α,
α,
∵∠ABD=∠ABC-∠DBC,∠DBC=60°,
∴∠ABD=30-![]() α,
α,
故答案为30-![]() α;
α;
(2)如图2,连接AD,CD,
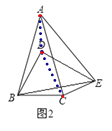
∵线段BC绕B逆时针旋转60°得到线段BD,
则BC=BD,∠DBC=60°,
∵∠ABE=60°,
∴∠ABD=60°-∠DBE=∠EBC=30°-![]() α,且△BCD为等边三角形,
α,且△BCD为等边三角形,
∴BD=CD,∠BDC=60°.
在△ABD与△ACD中,
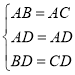 ,
,
∴△ABD≌△ACD,
∴∠BAD=∠CAD,∠ADB=∠ADC,
∵∠BDC=60°,
∴∠ADB=∠ADC=150°,
∴∠ADB=∠BCE.
∵∠ABD=60°-DBE, ∠CBE=60°-∠DBE,
∴∠ABD=∠EBC.
在△ABD和△EBC中
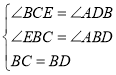 ,
,
∴△ABD≌△EBC(AAS),
∴∠EBC=∠ABD=30-![]() α.
α.
∵∠BCD=60°,∠BCE=150°,
∴∠DCE=150°-60°=90°,
∵∠DEC=45°,
∴△DEC为等腰直角三角形,
∴DC=CE=BC,
∵∠BCE=150°,
∴∠EBC=![]() (180°-150°)=15°,
(180°-150°)=15°,
∵∠EBC=30-![]() α=15,
α=15,
∴α=30°.
(3)△ABE是等边三角形,
由(2)知△ABD≌△EBC
∴AB=BE,
∵∠ABE=60°,
∴△ABE是等边三角形;


科目:初中数学 来源: 题型:
【题目】在不透明的口袋中,有四只形状、大小、质地完全相同的小球,四只小球上分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 、小明先从盒子里随机取出一只小球(不放回),记下数字作为平面直角坐标系内点的横坐标;再由小华随机取出一只小球,记下数字作为平面直角坐标系内点的纵坐标.
、小明先从盒子里随机取出一只小球(不放回),记下数字作为平面直角坐标系内点的横坐标;再由小华随机取出一只小球,记下数字作为平面直角坐标系内点的纵坐标.
![]() 用列表法或画树状图,表示所有这些点的坐标;
用列表法或画树状图,表示所有这些点的坐标;
![]() 小刚为小明、小华两人设计了一个游戏:当上述
小刚为小明、小华两人设计了一个游戏:当上述![]() 中的点在正比例函数
中的点在正比例函数![]() 图象上方时小明获胜,否则小华获胜、你认为这个游戏公平吗?请说明理由.
图象上方时小明获胜,否则小华获胜、你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,CE和BD交于点O,AO的延长线交BC于点F,则图中全等的三角形有( )

A.8对B.7对C.6对D.5对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题
例题:已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n),
则x2﹣4x+m=x2+(n+3)x+3n
∴![]()
解得:n=﹣7,m=﹣21.
∴另一个因式为(x﹣7),m的值为﹣21.
问题:
(1)若二次三项式x2﹣5x+6可分解为(x﹣2)(x+a),则a= ;
(2)若二次三项式2x2+bx﹣5可分解为(2x﹣1)(x+5),则b= ;
(3)仿照以上方法解答下面问题:若二次三项式2x2+3x﹣k有一个因式是(2x﹣5),求另一个因式以及k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC 中,∠ACB=90°,AC=80,BC=60, 点D 从点 B 出发,在线段 BA 上以每秒 4 个单位长度的速度向终点A 运动,连结CD. 设点D 运动的时间为 t 秒.
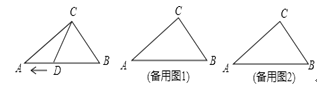
(1)用含 t 的代数式表示 BD 的长.
(2)求AB 的长及 AB 边上的高.
(3)当△BCD 为等腰三角形时,直接写出 t 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com