
����Ŀ����ͼ����ֱ������ϵƽ���ڣ�����y=![]() ��x��0��m�dz�������ͼ��A��1��4����B��a��b��������a��1������A��x��Ĵ��ߣ�����ΪC������B��y��Ĵ��ߣ�����ΪD������AD��AB��DC��CB��
��x��0��m�dz�������ͼ��A��1��4����B��a��b��������a��1������A��x��Ĵ��ߣ�����ΪC������B��y��Ĵ��ߣ�����ΪD������AD��AB��DC��CB��
��1��������������ʽ��
��2������ABD�����ΪS������a�Ĵ���ʽ��ʾ��S��
��3������ABD�����Ϊ2ʱ���ж��ı���ABCD����״����˵�����ɣ�

���𰸡���1����������������ʽΪy=![]() ����2��S=2a��2����3���ı���ABCDΪ���Σ����ɼ�����.
����2��S=2a��2����3���ı���ABCDΪ���Σ����ɼ�����.
�������������������1����A��1��4������y=![]() ���ô���ϵ������⼴�ɣ�
���ô���ϵ������⼴�ɣ�
��2����B��a��b��������1������ý���ʽ�У����b��a�Ĺ�ϵ�����������ε������ʽ��ʽ���ɣ�
��3����S=2���루2���еĽ���ʽ�У����a��ֵ����֪�ı���ABCD�ĶԽ����ഹֱƽ�֣��Ӷ���֤���ı���ABCDΪ����.
�⣺��1����A��1��4������y=![]() ��m=1��4=4��
��m=1��4=4��
���Է�������������ʽΪy=![]() ��
��
��2����B��a��b������y=![]() ��b=
��b=![]() ��
��
����S=![]() a��4��
a��4��![]() ��=2a��2��
��=2a��2��
��3���ı���ABCDΪ���Σ��������£�
��S=2ʱ��2a��2=2�����a=2��
����AC��BD���ഹֱƽ�֣�
�����ı���ABCDΪ���Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��x�ᡢy��ֱ��ڵ�A�͵�B����C���߶�AB�ϣ���D��y��ĸ������ϣ�C��D���㵽x��ľ����Ϊ2��
��x�ᡢy��ֱ��ڵ�A�͵�B����C���߶�AB�ϣ���D��y��ĸ������ϣ�C��D���㵽x��ľ����Ϊ2��
��1����C�������� ��������D�������� �� ����
��2����PΪ�߶�OA�ϵ�һ���㣬��PC+PD��Сʱ�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ACB����AED��Ϊ����ֱ�������Σ���AED=��ACB=90������D��AB�ϣ���CE��M��N�ֱ�ΪBD��CE���е㣮
��1����֤��MN��CE��
��2����ͼ2����AED��A����ʱ����ת30������֤��CE=2MN��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ͼ1��ʾ������ABC�У���ACB=90������A=30����BC=4����б��AB������CD����������μ�����AC1D1����BC2D2���������Σ���ͼ2��ʾ��������AC1D1��ֱ��D2B����ƽ�ƣ���A��D1��D2��Bʼ����ͬһֱ���ϣ�������D1�ڵ�B�غ�ʱ��ƽ��ֹͣ����ƽ�ƾ���D1D2Ϊx����AC1D1����BC2D2���ص��������Ϊy����y��x�ĺ���ͼ������ǣ�������

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y1��mx��ͼ���뷴��������y2��![]() (mΪ������m��0)��ͼ����һ������ĺ�������2��
(mΪ������m��0)��ͼ����һ������ĺ�������2��
(1)��m��ֵ��
(2)д����y1��y2ʱ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊacm���������ڣ���ȥ�����������εı߳�acmΪֱ���İ�Բ.(���½������)
(1)ͼ����Ӱ���ֵ��ܳ�Ϊ______cm��
(2)ͼ����Ӱ���ֵ����Ϊ________cm2��
(3)��a��2ʱ����ͼ����Ӱ���ֵ����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ�������ۼ�x��Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3���������Ҫ���ÿ�첻����1350Ԫ�������ҷ��ϳ����Լ��Ĺ涨����ô����Ʒÿǧ���ۼ۵�ȡֵ��Χ�Ƕ��٣���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
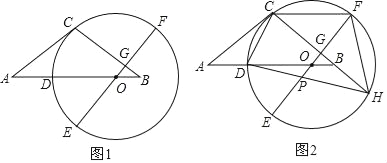
����Ŀ����ͼ1��������ABC�У�AC=BC����O��AB���ϣ���OΪԲ�ĵ�Բ������C����AB���ڵ�D��EFΪ��O��ֱ����EF��BC�ڵ�G����D��![]() ���е㣮
���е㣮
��1����֤��AC�ǡ�O�����ߣ�
��2����ͼ2���ӳ�CB����O�ڵ�H������HD��OE�ڵ�P������CF����֤��CF=DO+OP��
��3���ڣ�2���������£�����CD����tan��HDC=![]() ��CG=4����OP�ij���
��CG=4����OP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D�ǡ�ABC��һ�㣬��E��F��G��H�ֱ���AB��AC��CD��BD���е㡣
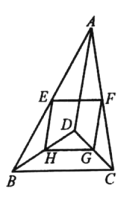
��1����֤���ı���EFGH��ƽ���ı��Σ���2����֪AD��6��BD��4��CD��3����BDC��90�㣬���ı���EFGH���ܳ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com