
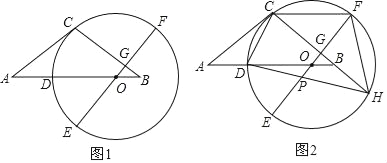
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是![]() 的中点.
的中点.
(1)求证:AC是⊙O的切线;
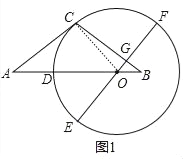
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
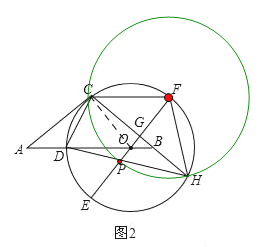
(3)在(2)的条件下,连接CD,若tan∠HDC=![]() ,CG=4,求OP的长.
,CG=4,求OP的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析: ![]() 连接OC.
连接OC. ![]() 得到
得到![]()
![]()
![]() 得出
得出![]() 即可证明AC是
即可证明AC是![]() 的切线.
的切线.
![]() 如图2中,连接OC,首先证明
如图2中,连接OC,首先证明![]() 再证明点P在以F为圆心FC为半径的圆上,即可解决问题;
再证明点P在以F为圆心FC为半径的圆上,即可解决问题;
![]() 在
在![]() 中,利用
中,利用![]() 求出
求出![]() 根据勾股定理求得
根据勾股定理求得![]()
![]() 在Rt
在Rt ![]() 中,根据勾股定理得,
中,根据勾股定理得, ![]() 利用
利用![]() 中的结论即可求出
中的结论即可求出![]() 的长度.
的长度.
试题解析:(1)证明:如图1中,连接OC.
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵点D是![]() 的中点,
的中点,
∴![]() =
=![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
∴AC是![]() 的切线,
的切线,
(2)证明:如图2中,连接OC,
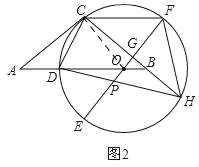
∵![]()
∴![]()
∴EF垂直平分HC,
∴![]()
∵![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴点P在以F为圆心FC为半径的圆上,
∴![]()
∵![]()
∴![]()
即![]()
(3)如图3,连接CO并延长交![]() 于M,连接
于M,连接![]() ,
,
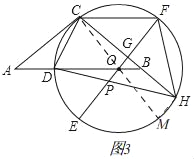
∴![]()
∵![]() 于G,
于G,
![]()
在![]() 中,
中, ![]()
∴![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴OG∥MH,
∵![]()
∴![]()
∴![]()
在Rt ![]() 中,根据勾股定理得,
中,根据勾股定理得, ![]()
由(2)知, ![]()


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系平面内,函数y=![]() (x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,AB,DC,CB.
(x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,AB,DC,CB.
(1)求反比例函数解析式;
(2)当△ABD的面积为S,试用a的代数式表示求S.
(3)当△ABD的面积为2时,判断四边形ABCD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法中不正确的是( )
,下列说法中不正确的是( )
A. 图像经过点(1.-2)
B. 图像分布在第二第四象限
C. x>0时,y随x增大而增大
D. 若点A(![]() )B(
)B(![]() )在图像上,若
)在图像上,若![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:点A、B在数轴上分别表示有理数a、b,![]() 表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①,
表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①,![]() ;
;
当A、B两点都在原点右侧时,如图②,![]() ;
;
当AB两点都在原点左侧时,如图③,![]() ;
;
当AB两点在原点两侧时,如图④,![]() ;
;

请根据上述结论,回答下列问题:
(1)数轴上表示2和5的两点问距离是______,数轴上表示2和-6的两点间距高是_________,数轴上表示-1和3的两点间距离是____________.
(2)数轴上表示x和-1的两点A和B之间的距离可表示为_________,若|AB|=2,则x的值为_____________.
(3)当![]() 取最小值时,请写出所有符合条件的x的整数值_______________.
取最小值时,请写出所有符合条件的x的整数值_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年3月,某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(x均为整数,总分100分),绘制了如下尚不完整的统计图表.
调查结果统计表
组别 | 成绩分组(单位:分) | 频数 | 频率 |
A | 80≤x<85 | 50 | 0.1 |
B | 85≤x<90 | 75 | |
C | 90≤x<95 | 150 | c |
D | 95≤x≤100 | a | |
合计 | b | 1 |
根据以上信息解答下列问题:
(1)统计表中,a=_____,b=_____,c=_____;
(2)扇形统计图中,m的值为_____,“C”所对应的圆心角的度数是_____;
(3)若参加本次竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接期中考试,小强对考试前剩余时间作了一个安排,他把计划复习重要内容的时间用一个四边形圈起来.如图,他发现,用这样的四边形圈起来五个数的和恰好是5的倍数,他又试了几个位置,都符合这样的特征。
(1)若设这五个数中间的数为a,请你用整式的加减说明其中的道理.
(2)这五个数的和能为150吗?若能,请写出中间那个数,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
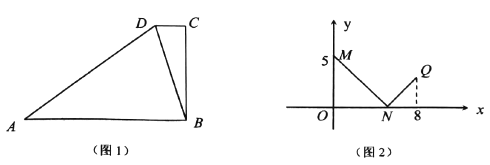
【题目】已知:梯形![]() 中,
中,![]() ,联结
,联结![]() (如图1). 点
(如图1). 点![]() 沿梯形的边从点
沿梯形的边从点![]() 移动,设点
移动,设点![]() 移动的距离为
移动的距离为![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 从点
从点![]() 移动到点
移动到点![]() 时,
时,![]() 与
与![]() 的函数关系(如图2)中的折线
的函数关系(如图2)中的折线![]() 所示. 试求
所示. 试求![]() 的长;
的长;
(3)在(2)的情况下,点![]() 从点
从点![]() 移动的过程中,
移动的过程中,![]() 是否可能为等腰三角形?若能,请求出所有能使
是否可能为等腰三角形?若能,请求出所有能使![]() 为等腰三角形的
为等腰三角形的![]() 的取值;若不能,请说明理由.
的取值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com