
【题目】计算:
①![]() ②
②![]()
③![]() ④
④![]()
⑤![]() ⑥
⑥![]()
⑦![]() ⑧
⑧![]()
【答案】①2;②-100;③-13;④1;⑤76;⑥-24;⑦-27;⑧-12.
【解析】
①根据减法法则把减法变为加法,然后根据有理数加法法则计算;
②把减法变为加法后,利用交换律和结合律进行简便运算;
③先算乘法,再算加减即可;
④利用乘法分配律计算即可;
⑤逆用乘法分配律计算即可;
⑥先把除法统一成乘法,然后从左到右依次计算即可;
⑦根据有理数混合运算法则计算即可;
⑧根据有理数混合运算法则计算即可.
①原式=![]() =4.3-2.3=2;
=4.3-2.3=2;
②原式=![]()
=![]()
=1+0+(-101)
=-100;
③原式=27-40=-13;
④原式=![]()
=6-4-3+2
=1;
⑤原式=![]()
=![]()
=76;
⑥原式=![]()
=-24;
⑦原式=![]()
=![]()
=-27;
⑧原式=![]()
=![]()
=![]()
=-12.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】下列说法,其中正确的有( )
①如果a大于b,那么a的倒数小于b的倒数;②若a与b互为相反数,则![]() =﹣
=﹣![]() ;③几个有理数相乘,负因数的个数是偶数时,积是正数;④如果mx=my,那么x=y,
;③几个有理数相乘,负因数的个数是偶数时,积是正数;④如果mx=my,那么x=y,
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.
与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.
(1)点C的坐标为 ,点D的坐标为 ;
(2)点P为线段OA上的一动点,当PC+PD最小时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,抛物线![]() 交x轴于点A(l,0)、B(3,0),交y轴于点C.
交x轴于点A(l,0)、B(3,0),交y轴于点C.
(1)如图1,求抛物线的解析式;
(2)如图2,点P为对称轴右侧第四象限抛物线上一点,连接PA并延长交y轴于点K,点P横坐标为t,△PCK的面积为S,求S与t的函数关系式(直接写出自变量t的取值范围);
(3)如图3,在(2)的条件下,过点A作AD⊥AP交y轴于点D.连接OP,过点O作OE⊥OP交AD延长线于点E,当OE=OP时,延长EA交抛物线于点Q,点M在直线EC上,连接QM,交AB于点H,将射线QM绕点Q逆时针旋转45°,得到射线QN交AB于点F,交直线EC于点N,若AH:HF=3:5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,在平面直角坐标系中如图所示:完成下列问题:

(1)画出△ABC绕点O逆时针旋转90后的△A![]() B
B![]() C
C![]() ;点B1的坐标为___;
;点B1的坐标为___;
(2)在(1)的旋转过程中,点B运动的路径长是___
(3)作出△ABC关于原点O对称的△A![]() B
B![]() C
C![]() ;点C
;点C![]() 的坐标为___.
的坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知长方形ABCD的边AD长为a,边AB长为b,正方形CEFG的边长为c,点G在边CD上.

(1)求△BDG的面积;
(2)求△BDF的面积;
(3)以点G为圆心,以c的长度为半径画弧,求图中阴影部分的面积.(注:以上各题均用字母a、b、c表示.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ACB、△AED都为等腰直角三角形,∠AED=∠ACB=90°,点D在AB上,连CE,M、N分别为BD、CE的中点.
(1)求证:MN⊥CE;
(2)如图2将△AED绕A点逆时针旋转30°,求证:CE=2MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(如图1所示)在△ABC中,∠ACB=90°,∠A=30°,BC=4,沿斜边AB的中线CD把这个三角形剪成△AC1D1和△BC2D2两个三角形(如图2所示).将△AC1D1沿直线D2B方向平移(点A,D1,D2,B始终在同一直线上),当点D1于点B重合时,平移停止.设平移距离D1D2为x,△AC1D1和△BC2D2的重叠部分面积为y,在y与x的函数图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
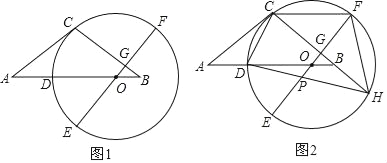
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是![]() 的中点.
的中点.
(1)求证:AC是⊙O的切线;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
(3)在(2)的条件下,连接CD,若tan∠HDC=![]() ,CG=4,求OP的长.
,CG=4,求OP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com