
����Ŀ����ƽ��ֱ������ϵ��,OΪ����ԭ��,������![]() ��x���ڵ�A(l,0)��B(3,0),��y���ڵ�C.
��x���ڵ�A(l,0)��B(3,0),��y���ڵ�C.
(1)��ͼ1,�������ߵĽ���ʽ��
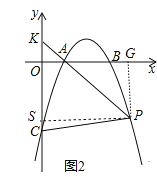
(2)��ͼ2,��PΪ�Գ����Ҳ����������������һ��,����PA���ӳ���y���ڵ�K,��P������Ϊt,��PCK�����ΪS,��S��t�ĺ�����ϵʽ(ֱ��д���Ա���t��ȡֵ��Χ����
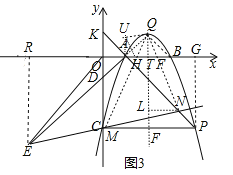
(3)��ͼ3,��(2)��������,����A��AD��AP��y���ڵ�D.����OP,����O��OE��OP��AD�ӳ����ڵ�E,��OE=OPʱ,�ӳ�EA���������ڵ�Q,��M��ֱ��EC��,����QM,��AB�ڵ�H��������QM�Ƶ�Q��ʱ����ת45��,�õ�����QN��AB�ڵ�F,��ֱ��EC�ڵ�N,��AH:HF=3:5,��![]() ��ֵ.
��ֵ.

���𰸡�(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
�������������������1�����ô���ϵ�������ɽ��������
��2������P��PG��x���ڵ�G��PS��y���ڵ�S�����CK��PS��ֵ���ɽ��������
��3������ȷ����Q��2��1����AT=BT=1���Ƴ���AQB=90�㣬����A��AU��x�� ����ȡAU=BF������QU���ɡ�QAU�ա�QBF���Ƴ���AQU=��BQF���Ƴ�QF=QU����HQU=��HQF=45�㣬QH=QH���Ƴ���QUH�ա�QHF���Ƴ�UH=HF����AH=3k����HF=5k����Rt��AUH����AU=3k���Ƴ�AH��HF��FB=3��5��4�Ƴ�AH=HT=![]() ��TF=
��TF=![]() tan��HQT=
tan��HQT=![]() tan��FQT=
tan��FQT=![]() ����ECֱ�߽���ʽΪy=kx+b ����E����3����4������C��0����3�����������ʽΪy=
����ECֱ�߽���ʽΪy=kx+b ����E����3����4������C��0����3�����������ʽΪy=![]() x��3������M��MV��QV ����N��NL��QV�ڵ�L ���M��x��
x��3������M��MV��QV ����N��NL��QV�ڵ�L ���M��x�� ![]() ��3������tan��HQT=
��3������tan��HQT=![]() =
=![]() �ɵ�x=0����M��0����3�����C�غ������N��n��
�ɵ�x=0����M��0����3�����C�غ������N��n�� ![]() n��3����tan��FQT=
n��3����tan��FQT=![]() =
=![]() ���n=3���ɵ�
���n=3���ɵ�![]() =
=![]() =
=![]() ��
��
���������������1����A��1��0����B��3��0�����������߽���ʽ���� ![]() �����
�����![]() ���������߽���ʽΪy=��x2+4x��3��
���������߽���ʽΪy=��x2+4x��3��
��2������P��PG��x���ڵ�G��PS��y���ڵ�S��
AG=t��1 GP=t2��4t+3����Rt��PAG����tan��PAG=![]() =
=![]() =t��3����Rt��AKO����tan��KAO=
=t��3����Rt��AKO����tan��KAO=![]() =
=![]() =t��3��OK=t��3����CK=t��3+3=t����S=
=t��3��OK=t��3����CK=t��3+3=t����S=![]() CKPS=
CKPS=![]() t2��t��3����
t2��t��3����
��3������E��ER��x���ڵ�R����OE��OP����REO=��POG��OE=OP����ERO=��OGP�����OER�ա�POG����OG=ER=t��OR=PG=t2��4t+3��AR=t2��4t+4����REA=��PAG��tan��REA=![]() =
=![]() ��tan��REA=tan��PAG��
��tan��REA=tan��PAG�� ![]() =t��3�������t=4�����E����3����4����P��4����3����CP��OG AR=ER=4�����EAR=��QAB=45�㣬����Q��QT��x���ڵ�T�����ӳ�CP�ڵ�V������QB�����Q��m����m2+4m��3������QT=span>AT �ɵé�m2+4m��3=m��1�����m=1��2�����Q��2��1����AT=BT=1�����AQB=90�㣬����A��AU��x�� ����ȡAU=BF������QU����QAU=��QBT=45�㣬QA=QB�����QAU�ա�QBF�����AQU=��BQF����QF=QU����HQU=��HQF=45�㣬QH=QH�����QUH�ա�QHF����UH=HF����AH=3k����HF=5k����Rt��AUH����AU=3k����AH��HF��FB=3��5��4����AH=HT=
=t��3�������t=4�����E����3����4����P��4����3����CP��OG AR=ER=4�����EAR=��QAB=45�㣬����Q��QT��x���ڵ�T�����ӳ�CP�ڵ�V������QB�����Q��m����m2+4m��3������QT=span>AT �ɵé�m2+4m��3=m��1�����m=1��2�����Q��2��1����AT=BT=1�����AQB=90�㣬����A��AU��x�� ����ȡAU=BF������QU����QAU=��QBT=45�㣬QA=QB�����QAU�ա�QBF�����AQU=��BQF����QF=QU����HQU=��HQF=45�㣬QH=QH�����QUH�ա�QHF����UH=HF����AH=3k����HF=5k����Rt��AUH����AU=3k����AH��HF��FB=3��5��4����AH=HT=![]() ��TF=
��TF=![]() tan��HQT=
tan��HQT=![]() tan��FQT=
tan��FQT=![]() ����ECֱ�߽���ʽΪy=kx+b ����E����3����4������C��0����3�����������ʽΪy=
����ECֱ�߽���ʽΪy=kx+b ����E����3����4������C��0����3�����������ʽΪy=![]() x��3������M��MV��QV ����N��NL��QV�ڵ�L ���M��x��
x��3������M��MV��QV ����N��NL��QV�ڵ�L ���M��x�� ![]() ��3������tan��HQT=
��3������tan��HQT=![]() =
=![]() ���ɵ�x=0����M��0����3�����C�غ������N��n��
���ɵ�x=0����M��0����3�����C�غ������N��n�� ![]() n��3����tan��FQT=
n��3����tan��FQT=![]() =
=![]() �������n=3����
�������n=3����![]() =
=![]() =
=![]() ��
��


 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н�����Ϊ���˽����ѧ��ÿѧ�ڲμ��ۺ�ʵ�����������������������ijУ����ѧ��һ��ѧ�ڲμ��ۺ�ʵ��������������õõ������ݻ���������������������ͳ��ͼ���������ͼ���ṩ����Ϣ���ش��������⣺

��1������ͳ��ͼ��a��ֵΪ�� ����
��2����ȫƵ���ֲ�ֱ��ͼ��
��3������γ��������У��������� ���죬��λ������ ���죻
��4��������Ƹ��г���ѧ��ÿѧ�ڲμ��ۺ�ʵ�����ƽ������Լ�Ƕ��٣����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ո������һ��ѧϰ�ɼ����쵫����һ�������ͬѧδ����ѣ��Ѿ�Ϊ�����������п���������.����ĩ���ڼ���ϰ1������������ÿ����150��Ϊ������������IJ��ֱַ�������������ʾ��8�γɼ�����λ���£��ֱ��ǣ�10����8����5����2����2����8����3����4.
��1���ɼ���õ�һ�α�����һ�ζ��������£�
��2����������8��������ƽ���ɼ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��9��6�գ�������������������ʽ��ҵ���������������ʳ���Ƴ���A��B�����ײͺ�������ʳ�����죬A�ײ͵����۶�ռ�����۶��40%��B�ײ͵����۶�ռ�����۶��20%�������ڼ䣬���������ÿ����ӣ��˵��ϰ忼�������ο͵���ʳ��ζ�Ƴ���C�ײͣ���10��1����һ�죬A��B�ײ��Ե����۶��9��6�յ����۶������15%��C�ײ͵����۶�ռ10��1�յ��������۶��20%��������ʳ�����۶�䣬��10��1�յ������۶��9��6�յ������۶�����__________%.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,���ı���ABCD��,AD=5,CD=3,��ABC=��ACB=��ADC=45��,��BD�ij�Ϊ����

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������⣺
��1����һ������60�����������ǵȱ������Σ�
��2�������������ĺͲ�һ������������
��3������һ������100��������Ϊ8cm����������������ȫ�ȣ�
��4������mΪ��ֵ������x�ķ���x2+mx��m��1=0�ض���ʵ����������������ĸ���Ϊ��������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ6����B����������A������һ�㣬��A��B�����ľ���Ϊ10������P�ӵ�A��������ÿ��3����λ���ȵ��ٶ������������˶���
![]()
��1�������ϵ�B��ʾ�������� ����
��2���˶�1��ʱ����P��ʾ�������� ����
��3������Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ������������˶�������P��Qͬʱ��������
�ٵ���P�˶�������ʱ����P���Q����������ʱ��Ӧ���������Ƕ��٣�
�ڵ���P�˶�������ʱ����P���Q�ľ���Ϊ8����λ���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڷ���������![]() ������˵���в���ȷ���ǣ� ��
������˵���в���ȷ���ǣ� ��
A. ͼ���㣨1.-2��
B. ͼ��ֲ��ڵڶ���������
C. x>0ʱ��y��x���������
D. ����A��![]() ��B��
��B��![]() ����ͼ���ϣ���
����ͼ���ϣ���![]() ,��
,��![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com