
【题目】有下列命题:
(1)有一个角是60°的三角形是等边三角形;
(2)两个无理数的和不一定是无理数;
(3)各有一个角是100°,腰长为8cm的两个等腰三角形全等;
(4)不论m为何值,关于x的方程x2+mx﹣m﹣1=0必定有实数根.其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】(1)有一个角是60°的三角形是等边三角形;根据等腰三角形的判定,有一个角是60°,的等腰三角形是等边三角形,故本选项正确;
(2)两个无理数的和不一定是无理数;∵![]() +(﹣
+(﹣![]() )=0,∴两个无理数的和不一定是无理数,故本选项正确;
)=0,∴两个无理数的和不一定是无理数,故本选项正确;
(3)各有一个角是100°,腰长为8cm的两个等腰三角形全等;根据等腰三角形的性质,此三角形一定是顶角是100°,腰长为8cm的两个等腰三角形一定全等,故本选项正确;
(4)不论m为何值,关于x的方程x2+mx﹣m﹣1=0必定有实数根.∵b2﹣4ac=m2﹣4(﹣m﹣1)=(m+2)2≥0,∴不论m为何值,关于x的方程x2+mx﹣m﹣1=0必定有实数根,故本选项正确;
其中真命题的个数为4个.
故选D.


科目:初中数学 来源: 题型:
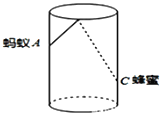
【题目】如图,圆柱形玻璃杯,高为![]() ,底面周长为
,底面周长为![]() ,在杯内离杯底
,在杯内离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿![]() 与蜂蜜相对的点
与蜂蜜相对的点![]() 处,则蚂蚁到达蜂蜜的最短距离为( )
处,则蚂蚁到达蜂蜜的最短距离为( )![]() .
.
A. 15B. ![]() C. 12D. 18
C. 12D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中1张餐桌可坐6人,有以下两种摆放方式:
(1)对于方式一:4张桌子拼在一起可坐 人;对于方式二,n张桌子拼在一起可坐 人;
(2)该餐厅有40张这样的长方形桌子,若按方式一每5张拼成一张大桌子,则40张桌子可拼成8张大桌子,共可坐多少人?
(3)在(2)中,若改成每8张拼成一张大桌子,按方式二的拼法,则40张桌子共可坐多少人?
(4)一天中午,该餐厅来了98位顾客共同就餐,要求用满座位,但餐厅中只有25张这样的长方形桌子可用,若你是这家餐厅的经理,你打算选择哪种方式来摆餐桌呢(不考虑场地等因素)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个小球,分别标有数字2,3,4,![]() ,这些球除数字外都相同.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和.记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表:
,这些球除数字外都相同.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和.记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表:
摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为7”出现的频数 | 1 | 9 | 14 | 24 | 26 | 37 | 58 | 82 | 109 | 150 |
“和为7”出现的频率 | 0.10 | 0.45 | 0.47 | 0.40 | 0.29 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
试估计出现“和为7”的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,抛物线![]() 交x轴于点A(l,0)、B(3,0),交y轴于点C.
交x轴于点A(l,0)、B(3,0),交y轴于点C.
(1)如图1,求抛物线的解析式;
(2)如图2,点P为对称轴右侧第四象限抛物线上一点,连接PA并延长交y轴于点K,点P横坐标为t,△PCK的面积为S,求S与t的函数关系式(直接写出自变量t的取值范围);
(3)如图3,在(2)的条件下,过点A作AD⊥AP交y轴于点D.连接OP,过点O作OE⊥OP交AD延长线于点E,当OE=OP时,延长EA交抛物线于点Q,点M在直线EC上,连接QM,交AB于点H,将射线QM绕点Q逆时针旋转45°,得到射线QN交AB于点F,交直线EC于点N,若AH:HF=3:5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题。
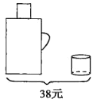
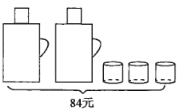
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知长方形ABCD的边AD长为a,边AB长为b,正方形CEFG的边长为c,点G在边CD上.

(1)求△BDG的面积;
(2)求△BDF的面积;
(3)以点G为圆心,以c的长度为半径画弧,求图中阴影部分的面积.(注:以上各题均用字母a、b、c表示.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某淘宝店家为迎接“双十一”抢购活动,在甲批发市场以每件a元的价格进了40件童装,又在乙批发市场以每件b元(a>b)的价格进了同样的60件童装.如果店家以每件![]() 元的价格卖出这款童装,卖完后,这家商店( )
元的价格卖出这款童装,卖完后,这家商店( )
A.盈利了B.亏损了
C.不赢不亏D.盈亏不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设0!表示自然数由1到n的连乘积,并规定0!=1,Anm=![]() ,nm=
,nm=![]() (n≥0,n≥m)例如1!=1,2!=1×2=2,3!=1×2×3=6,A53=
(n≥0,n≥m)例如1!=1,2!=1×2=2,3!=1×2×3=6,A53=![]() =60,C64=
=60,C64=![]() =15,请回答以下问题:
=15,请回答以下问题:
(1)求C32,A32;
(2)试根据C32,A32,2!的值写出C32,A32,2!满足的等量关系;试根据C43,A43,3!的值写出C43,A43,3!满足的等量关系;试根据C54,A54,4!的值写出C54,A54,4!满足的等量关系;
(3)探究Amn,Cmn与n!之间满足的等量关系(不需要证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com