
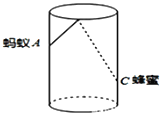
【题目】如图,圆柱形玻璃杯,高为![]() ,底面周长为
,底面周长为![]() ,在杯内离杯底
,在杯内离杯底![]() 的点
的点![]() 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿![]() 与蜂蜜相对的点
与蜂蜜相对的点![]() 处,则蚂蚁到达蜂蜜的最短距离为( )
处,则蚂蚁到达蜂蜜的最短距离为( )![]() .
.
A. 15B. ![]() C. 12D. 18
C. 12D. 18
科目:初中数学 来源: 题型:
【题目】王先生到泉州台商投资区行政服务中心大楼办事,假定乘电梯向上一楼记作+1,向下一楼记作﹣1,王先生从1楼出发,电梯上下楼层依次记录如下:(单位:层)
+6,﹣3,+10,﹣8,+12,﹣7,﹣10.
(1)请你通过计算说明王先生最后是否回到出发点1楼.
(2)该中心大楼每层高3m,电梯每向上或下1m需要耗电0.1度,根据王先生现在所处位置,请你算算,他办事时电梯需要耗电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“最美数学小报”的评比中,校团委给每个同学的作品打分,成绩分为![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
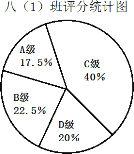

请你根据以上提供的信息解答下列问题:
(1)将表格补充完整.
平均数(分) | 中位数(分) | 众数(分) | |
八(1)班 | 83.75 | 80 | |
八(2)班 | 80 |
(2)若八(1)班有40人,且评分为B级及以上的同学有纪念奖章,请问该班共有几位同学得到奖章?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东昌湖举行的健身运动会龙舟比赛中,甲、乙两队在500米的赛道上,所滑行的路程y(m)与实践x(min)之间的函数关系如图所示,下列说法正确的有____________.

①乙队比甲队提前0. 25min到达终点.
②当乙队划行110m时,此时落后甲队15m.
③0. 5min后,乙队比甲队每分钟快40m.
④自1. 5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到255m/min.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育局为了了解初二学生每学期参加综合实践活动的情况,随机抽样调查了某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图.请你根据图中提供的信息,回答下列问题:

(1)扇形统计图中a的值为 ;
(2)补全频数分布直方图;
(3)在这次抽样调查中,众数是 天,中位数是 天;
(4)请你估计该市初二学生每学期参加综合实践活动的平均天数约是多少?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一种型号的电脑报价均为6000元,并且多买都有一定的优惠.各商场的优惠条件如下表所示:
商场 | 优惠条件 |
甲商场 | 第一台按原价收费,其余的每台优惠25% |
乙商场 | 每台优惠20% |
(1)设学校购买![]() 台电脑,选择甲商场时,所需费用为
台电脑,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)什么情况下,两家商场的收费相同?什么情况下,到甲商场购买更优惠?什么情况下,到乙商场购买更优惠?
(3)现在因为急需,计划从甲乙两商场一共买入10台电脑,已知甲商场的运费为每台50元,乙商场的运费为每台60元,设总运费为![]() 元,从甲商场购买
元,从甲商场购买![]() 台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
台电脑,在甲商场的库存只有4台的情况下,怎样购买,总运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列命题:
(1)有一个角是60°的三角形是等边三角形;
(2)两个无理数的和不一定是无理数;
(3)各有一个角是100°,腰长为8cm的两个等腰三角形全等;
(4)不论m为何值,关于x的方程x2+mx﹣m﹣1=0必定有实数根.其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com