
【题目】阅读下面材料:点A、B在数轴上分别表示有理数a、b,![]() 表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①,
表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①,![]() ;
;
当A、B两点都在原点右侧时,如图②,![]() ;
;
当AB两点都在原点左侧时,如图③,![]() ;
;
当AB两点在原点两侧时,如图④,![]() ;
;

请根据上述结论,回答下列问题:
(1)数轴上表示2和5的两点问距离是______,数轴上表示2和-6的两点间距高是_________,数轴上表示-1和3的两点间距离是____________.
(2)数轴上表示x和-1的两点A和B之间的距离可表示为_________,若|AB|=2,则x的值为_____________.
(3)当![]() 取最小值时,请写出所有符合条件的x的整数值_______________.
取最小值时,请写出所有符合条件的x的整数值_______________.
【答案】(1)3,8,4;(2)|x+1|或|x-(-1)|或|-1-x|,1或-3;(3)-2,-1,0,1
【解析】
(1)根据材料中的知识可以得到两点之间的距离就是较大的数与较小的数的差,据此即可求解;
(2)根据材料中的知识,即可直接写出结果;
(3)代数式|x-1|+|x+2|表示数轴上一点到1、-2两点的距离的和,根据两点之间线段最短,进而得出答案.
解:(1)数轴上表示2和5的两点之间的距离是:5-2=3;
数轴上表示2和-6的两点之间的距离是2-(-6)=8,
数轴上表示1和-3的两点之间的距离是1-(-3)=4;
故答案为:3;8;4;
(2)数轴上表示x和-1的两点之间的距离是|x+1|,
|AB|=2,则|x+1|=2,故x=1或-3;
故答案为:|x+1|,1或-3;
(3)若|x+1|+|x-2|取最小值,那么表示x的点M在-1和2之间的线段上,
所以x的整数值是-2,-1,0,1;
故答案为:-2,-1,0,1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,在平面直角坐标系中如图所示:完成下列问题:

(1)画出△ABC绕点O逆时针旋转90后的△A![]() B
B![]() C
C![]() ;点B1的坐标为___;
;点B1的坐标为___;
(2)在(1)的旋转过程中,点B运动的路径长是___
(3)作出△ABC关于原点O对称的△A![]() B
B![]() C
C![]() ;点C
;点C![]() 的坐标为___.
的坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y1=mx的图象与反比例函数y2=![]() (m为常数,m≠0)的图象有一个交点的横坐标是2.
(m为常数,m≠0)的图象有一个交点的横坐标是2.
(1)求m的值;
(2)写出当y1<y2时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像经过点A(-1,0),并与反比例函数
的图像经过点A(-1,0),并与反比例函数![]() (
(![]() )的图像交于B(m,4)
)的图像交于B(m,4)

(1)求![]() 的值;
的值;
(2)以AB为一边,在AB的左侧作正方形![]() ,求C点坐标;
,求C点坐标;
(3)将正方形![]() 沿着
沿着![]() 轴的正方向,向右平移n个单位长度,得到正方形
轴的正方向,向右平移n个单位长度,得到正方形![]() ,线段
,线段![]() 的中点为点
的中点为点![]() ,若点
,若点![]() 和点
和点![]() 同时落在反比例函数
同时落在反比例函数![]() 的图像上,求n的值.
的图像上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
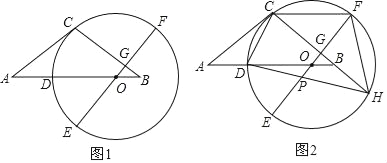
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是![]() 的中点.
的中点.
(1)求证:AC是⊙O的切线;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
(3)在(2)的条件下,连接CD,若tan∠HDC=![]() ,CG=4,求OP的长.
,CG=4,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快城市群的建设与发展,在A、B两城市间新建一条城际铁路,建成后,铁路运行里程由现在的210km缩短至180km,平均时速要比现行的平均时速快200km,运行时间仅是现行时间的![]() ,求建成后的城际铁路在A、B两地的运行时间?
,求建成后的城际铁路在A、B两地的运行时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形纸片ABCD沿对角线BD向上折叠,点C落在点E处,BE交AD于点F.


(1)求证:BF=DF;
(2)如图2,过点D作DG∥BE交BC于点G,连接FG交BD于点O,若AB=6,AD=8,求FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com