
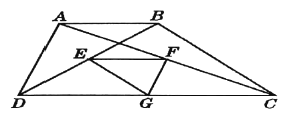
【题目】如图,梯形![]() 中,
中,![]() ,点
,点![]() 分别是
分别是![]() 的中点. 已知两底之差是6,两腰之和是12,则
的中点. 已知两底之差是6,两腰之和是12,则![]() 的周长是____.
的周长是____.
【答案】9.
【解析】
延长EF交BC于点H,可知EF,FH,FG、EG分别为△BDC、△ABC、△BDC和△ACD的中位线,由三角形中位线定理结合条件可求得EF+FG+EG,可求得答案.
连接AE,并延长交CD于K,
∵AB∥CD,
∴∠BAE=∠DKE,∠ABD=∠EDK,
∵点E、F、G分别是BD、AC、DC的中点.
∴BE=DE,
在△AEB和△KED中,
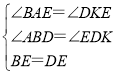 ,
,
∴△AEB≌△KED(AAS),
∴DK=AB,AE=EK,EF为△ACK的中位线,
∴EF=![]() CK=
CK=![]() (DC-DK)=
(DC-DK)=![]() (DC-AB),
(DC-AB),
∵EG为△BCD的中位线,∴EG=![]() BC,
BC,
又FG为△ACD的中位线,∴FG=![]() AD,
AD,
∴EG+GF=![]() (AD+BC),
(AD+BC),
∵两腰和是12,即AD+BC=12,两底差是6,即DC-AB=6,
∴EG+GF=6,FE=3,
∴△EFG的周长是6+3=9.
故答案为:9.


科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如图:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s=![]() t2+bt+c(b,c是常数)刻画.
t2+bt+c(b,c是常数)刻画.
(1)求m的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v0+![]() (t﹣30),v0是加速前的速度).
(t﹣30),v0是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:点A、B在数轴上分别表示有理数a、b,![]() 表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①,
表示A、B两点之间的距离。当A、B两点中有一点在原点时(假设A在原点),如图①,![]() ;
;
当A、B两点都在原点右侧时,如图②,![]() ;
;
当AB两点都在原点左侧时,如图③,![]() ;
;
当AB两点在原点两侧时,如图④,![]() ;
;

请根据上述结论,回答下列问题:
(1)数轴上表示2和5的两点问距离是______,数轴上表示2和-6的两点间距高是_________,数轴上表示-1和3的两点间距离是____________.
(2)数轴上表示x和-1的两点A和B之间的距离可表示为_________,若|AB|=2,则x的值为_____________.
(3)当![]() 取最小值时,请写出所有符合条件的x的整数值_______________.
取最小值时,请写出所有符合条件的x的整数值_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接期中考试,小强对考试前剩余时间作了一个安排,他把计划复习重要内容的时间用一个四边形圈起来.如图,他发现,用这样的四边形圈起来五个数的和恰好是5的倍数,他又试了几个位置,都符合这样的特征。
(1)若设这五个数中间的数为a,请你用整式的加减说明其中的道理.
(2)这五个数的和能为150吗?若能,请写出中间那个数,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+
x+![]() 与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )
与x轴、y轴分别交于点A、B,在坐标轴上找点P,使△ABP为等腰三角形,则点P的个数为( )

A. 2B. 4C. 6D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
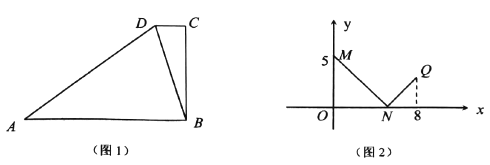
【题目】已知:梯形![]() 中,
中,![]() ,联结
,联结![]() (如图1). 点
(如图1). 点![]() 沿梯形的边从点
沿梯形的边从点![]() 移动,设点
移动,设点![]() 移动的距离为
移动的距离为![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 从点
从点![]() 移动到点
移动到点![]() 时,
时,![]() 与
与![]() 的函数关系(如图2)中的折线
的函数关系(如图2)中的折线![]() 所示. 试求
所示. 试求![]() 的长;
的长;
(3)在(2)的情况下,点![]() 从点
从点![]() 移动的过程中,
移动的过程中,![]() 是否可能为等腰三角形?若能,请求出所有能使
是否可能为等腰三角形?若能,请求出所有能使![]() 为等腰三角形的
为等腰三角形的![]() 的取值;若不能,请说明理由.
的取值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:

(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=-3x+3与坐标轴分别交于A,B两点,以线段AB为边,在第一象限内作正方形ABCD,直线y=3x-2与y轴交于点F,与线段AB交于点E,将正方形ABCD沿x轴负半轴方向平移a个单位长度,使点D落在直线EF上.有下列结论:①△ABO的面积为3;②点C的坐标是(4,1);③点E到x轴距离是![]() ;
;
④a=1.其中正确结论的个数是( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图的数阵由88个偶数排成.现用一个如图所示的平行四边形框可以框出四个数;
①图中平行四边形框内的四个数有什么关系?
②在数阵中任意作一类似(1)中的平行四边形框,设其中左上角的一个数是![]() ,那么其他三个数怎样表示?
,那么其他三个数怎样表示?
③在这个数阵的平行四边形框内,是否存在和为288的四个数?若存在,求出这四个数;不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com