
【题目】如图,点D是△ABC内一点,点E,F,G,H分别是AB,AC,CD,BD的中点。
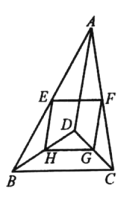
(1)求证:四边形EFGH是平行四边形;(2)已知AD=6,BD=4,CD=3,∠BDC=90°,求四边形EFGH的周长。
【答案】(1)见解析;(2)周长为:11.
【解析】
(1)根据三角形的中位线的定理和平行四边形的判定即可解答;
(2)利用勾股定理列式求出BC的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=![]() AD,EF=GH=
AD,EF=GH=![]() BC,然后代入数据进行计算即可得解.
BC,然后代入数据进行计算即可得解.
(1)证明:∵点E,F 分别是AB,AC 的中点,
∴EF 是△ABC 的中位线,∴EF∥BC 且EF=![]() BC;
BC;
又∵点H,G 分别是BD,CD 的中点,∴HG 是△BCD 的中位线,∴HG∥BC
且HG=![]() BC;
BC;
∴EF∥HG 且EF=HG,∴四边形EFGH 是平行四边形.
(2)∵点E,H 分别是AB,BD 的中点,∴EH 是△ABD 的中位线,∴EH=![]() AD=3;
AD=3;
∵∠BDC=90°,∴△BCD 是直角三角形;
在Rt△BCD 中,CD=3,BD=4,∴由勾股定理得:BC=5;
∵HG=![]() BC,∴HG=
BC,∴HG=![]() ;
;
由(1)知,四边形EFGH 是平行四边形,∴周长为2EH+2HG=11.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系平面内,函数y=![]() (x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,AB,DC,CB.
(x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,AB,DC,CB.
(1)求反比例函数解析式;
(2)当△ABD的面积为S,试用a的代数式表示求S.
(3)当△ABD的面积为2时,判断四边形ABCD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接期中考试,小强对考试前剩余时间作了一个安排,他把计划复习重要内容的时间用一个四边形圈起来.如图,他发现,用这样的四边形圈起来五个数的和恰好是5的倍数,他又试了几个位置,都符合这样的特征。
(1)若设这五个数中间的数为a,请你用整式的加减说明其中的道理.
(2)这五个数的和能为150吗?若能,请写出中间那个数,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:梯形![]() 中,
中,![]() ,联结
,联结![]() (如图1). 点
(如图1). 点![]() 沿梯形的边从点
沿梯形的边从点![]() 移动,设点
移动,设点![]() 移动的距离为
移动的距离为![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 从点
从点![]() 移动到点
移动到点![]() 时,
时,![]() 与
与![]() 的函数关系(如图2)中的折线
的函数关系(如图2)中的折线![]() 所示. 试求
所示. 试求![]() 的长;
的长;
(3)在(2)的情况下,点![]() 从点
从点![]() 移动的过程中,
移动的过程中,![]() 是否可能为等腰三角形?若能,请求出所有能使
是否可能为等腰三角形?若能,请求出所有能使![]() 为等腰三角形的
为等腰三角形的![]() 的取值;若不能,请说明理由.
的取值;若不能,请说明理由.
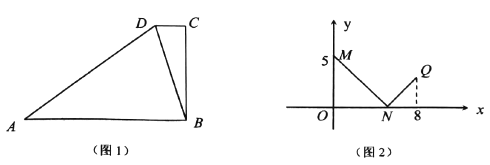
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图:

(1)本次被调查的学生有 名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,AB=CD.
(1)如图(1),求证:AD∥BC;
(2)如图(2),点F是AC的中点,弦DG∥AB,交BC于点E,交AC于点M,求证:AE=2DF;
(3)在(2)的条件下,若DG平分∠ADC,GE=5![]() ,tan∠ADF=4
,tan∠ADF=4![]() ,求⊙O的半径。
,求⊙O的半径。
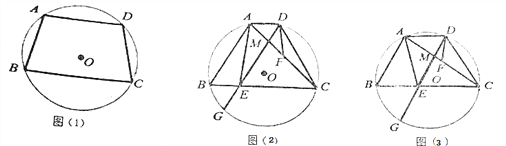
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=-3x+3与坐标轴分别交于A,B两点,以线段AB为边,在第一象限内作正方形ABCD,直线y=3x-2与y轴交于点F,与线段AB交于点E,将正方形ABCD沿x轴负半轴方向平移a个单位长度,使点D落在直线EF上.有下列结论:①△ABO的面积为3;②点C的坐标是(4,1);③点E到x轴距离是![]() ;
;
④a=1.其中正确结论的个数是( )

A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD 相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.
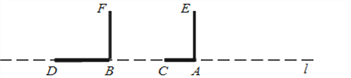
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com