
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:H为CE的中点;
(3)若BC=10,cosC=![]() ,求AE的长.
,求AE的长.

【答案】(1)相切;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)连结OD、AD,如图,先利用圆周角定理得到∠ADB=90°,则根据等腰三角形的性质得BD=CD,再证明OD为△ABC的中位线得到OD∥AC,加上DH⊥AC,所以OD⊥DH,然后根据切线的判定定理可判断DH为⊙O的切线;
(2)连结DE,如图,有圆内接四边形的性质得∠DEC=∠B,再证明∠DEC=∠C,然后根据等腰三角形的性质得到CH=EH;
(3)利用余弦的定义,在Rt△ADC中可计算出AC=![]() ,在Rt△CDH中可计算出CH=
,在Rt△CDH中可计算出CH=![]() ,则CE=2CH=
,则CE=2CH=![]() ,然后计算AC﹣CE即可得到AE的长.
,然后计算AC﹣CE即可得到AE的长.
试题解析:(1)DH与⊙O相切.理由如下:
连结OD、AD,如图,∵AB为直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴BD=CD,而AO=BO,∴OD为△ABC的中位线,∴OD∥AC,∵DH⊥AC,∴OD⊥DH,∴DH为⊙O的切线;
(2)证明:连结DE,如图,∵四边形ABDE为⊙O的内接四边形,∴∠DEC=∠B,∵AB=AC,∴∠B=∠C,∴∠DEC=∠C,∵DH⊥CE,∴CH=EH,即H为CE的中点;
(3)解:在Rt△ADC中,CD=![]() BC=5,∵cosC=
BC=5,∵cosC=![]() =
=![]() ,∴AC=
,∴AC=![]() ,在Rt△CDH中,∵cosC=
,在Rt△CDH中,∵cosC=![]() =
=![]() ,∴CH=
,∴CH=![]() ,∴CE=2CH=
,∴CE=2CH=![]() ,∴AE=AC﹣CE=
,∴AE=AC﹣CE=![]() =
=![]() .
.



科目:初中数学 来源: 题型:
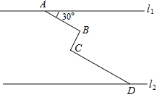
【题目】如图,在同一平面内,两条平行高速公路![]() 和
和![]() 间有一条“
间有一条“![]() ”型道路连通,其中
”型道路连通,其中![]() 段与高速公路
段与高速公路![]() 成
成![]() 角,长为
角,长为![]() ;
;![]() 段与
段与![]() 、
、![]() 段都垂直,
段都垂直,![]() 段长为
段长为![]() ,
,![]() 段长为
段长为![]() .则两条高速公路
.则两条高速公路![]() 和
和![]() 间的距离为________米(结果保留根号).
间的距离为________米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,
,![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上截取
上截取![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形;
是菱形;
![]() 如图
如图![]() ,
,![]() 中,
中,![]() 平分
平分![]() 的外角
的外角![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在
,在![]() 的延长线上截取
的延长线上截取![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .四边形
.四边形![]() 还是菱形吗?如果是,请证明;如果不是,请说明理由.
还是菱形吗?如果是,请证明;如果不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,在正方形
,在正方形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,垂足为
,垂足为![]() ,那么
,那么![]() 与
与![]() ________(“相等”或“不相等”)26.
________(“相等”或“不相等”)26.
![]() 如图
如图![]() ,将边长为
,将边长为![]() 的正方形纸片
的正方形纸片![]() 沿
沿![]() 折叠,使得点
折叠,使得点![]() 落到边
落到边![]() 上.若
上.若![]() ,求出
,求出![]() 和
和![]() 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍.
(1)求降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于900元的资金再次购进两种鲜花共500枝,康乃馨进价为2元/枝,玫瑰进价为1.5元/枝,问至少购进玫瑰多少枝?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的商品市场指导价为每千克![]() 元,公司的实际销售价格可以浮动
元,公司的实际销售价格可以浮动![]() 个百分点(即销售价格
个百分点(即销售价格![]() ),经过市场调研发现,这种商品的日销售量
),经过市场调研发现,这种商品的日销售量![]() (千克)与销售价格浮动的百分点
(千克)与销售价格浮动的百分点![]() 之间的函数关系为
之间的函数关系为![]() .若该公司按浮动
.若该公司按浮动![]() 个百分点的价格出售,每件商品仍可获利
个百分点的价格出售,每件商品仍可获利![]() .
.
![]() 求该公司生产销售每千克商品的成本为多少元?
求该公司生产销售每千克商品的成本为多少元?
![]() 当该公司的商品定价为多少元时,日销售利润为
当该公司的商品定价为多少元时,日销售利润为![]() 元?(说明:日销售利润
元?(说明:日销售利润![]() (销售价格一成本)
(销售价格一成本)![]() 日销售量)
日销售量)
![]() 该公司决定每销售一千克商品就捐赠
该公司决定每销售一千克商品就捐赠![]() 元利润
元利润![]() 给希望工程,公司通过销售记录发现,当价格浮动的百分点大于
给希望工程,公司通过销售记录发现,当价格浮动的百分点大于![]() 时,扣除捐赠后的日销售利润随
时,扣除捐赠后的日销售利润随![]() 的增大而减小,直接写出
的增大而减小,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,现给出以下四个结论:(1)AE=CF;(2)△EPF是等腰直角三角形;(3)S四边形AEPF=![]() S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )
S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )

A.1个B.3个C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com