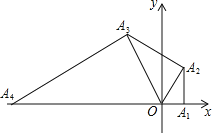
【题目】如图，在平面直角坐标系中，点
的坐标为
，以
为直角边作
，并使
，再以
为直角边作
，并使
，再以
为直角边作
，并使
…按此规律进行下去，则点
的坐标为_______．
【答案】
【解析】
通过解直角三角形，依次求
各点的坐标，再从其中找出规律，便可得结论．
解：由题意得，
的坐标为
，
的坐标为
，
的坐标为
，
的坐标为
，
的坐标为
，
的坐标为
，
的坐标为
，
…
由上可知，A点的方位是每6个循环，
与第一点方位相同的点在x正半轴上，其横坐标为
，其纵坐标为0，
与第二点方位相同的点在第一象限内，其横坐标为
，纵坐标为
，
与第三点方位相同的点在第二象限内，其横坐标为
，纵坐标为，
与第四点方位相同的点在x负半轴上，其横坐标为
，纵坐标为0，
与第五点方位相同的点在第三象限内，其横坐标为，纵坐标为
，
与第六点方位相同的点在第四象限内，其横坐标为，纵坐标为，
∴点
的方位与点
的方位相同，在第二象限内，其横坐标为
，纵坐标为
故答案为：．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，抛物线y＝﹣x2+6x﹣5与x轴交于A，B两点（点A在点B左边），与y轴交于点C．点P是抛物线上一个动点，过点P作x轴的垂线，垂足为点H，交直线BC于点E．
（1）求点A，B，C的坐标；
（2）连接CP，当CP平分∠OCB时，求点P的坐标；
（3）平面直角坐标系内是否存在点Q，使得以点P，E，B，Q为顶点的四边形为菱形？若存在，直接写出点Q的坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
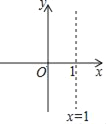
【题目】在平面直角坐标系中，抛物线y＝x2﹣2x+c（c为常数）的对称轴如图所示，且抛物线过点C（0，c）．
（1）当c＝﹣3时，点（x1，y1）在抛物线y＝x2﹣2x+c上，求y1的最小值；
（2）若抛物线与x轴有两个交点，自左向右分别为点A、B，且OA＝
OB，求抛物线的解析式；
（3）当﹣1＜x＜0时，抛物线与x轴有且只有一个公共点，求c的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
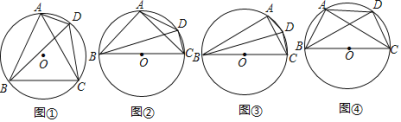
【题目】(1)方法选择
如图①，四边形
是
的内接四边形，连接
，
，
．求证：
.
小颖认为可用截长法证明：在
上截取
，连接
…
小军认为可用补短法证明：延长
至点
，使得
…
请你选择一种方法证明．
(2)类比探究
（探究1）
如图②，四边形是的内接四边形，连接，，
是的直径，
．试用等式表示线段
，，之间的数量关系，并证明你的结论．
（探究2）
如图③，四边形是的内接四边形，连接，．若是的直径，
，则线段，，之间的等量关系式是______．
(3)拓展猜想
如图④，四边形是的内接四边形，连接，．若是的直径，
，则线段，，之间的等量关系式是______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】中华文明，源远流长；中华汉字，寓意深广．为传承中华优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛．为了解本次大赛的成绩，校团委随机抽取了其中200名学生的成绩作为样本进行统计，制成如下不完整的统计图表：
频数频率分布表
成绩x（分） | 频数（人） | 频率 |
50≤x＜60 | 10 | 0.05 |
60≤x＜70 | 30 | 0.15 |
70≤x＜80 | 40 | n |
80≤x＜90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根据所给信息，解答下列问题：
（1）m= ，n= ；
（2）补全频数分布直方图；
（3）这200名学生成绩的中位数会落在 分数段；
（4）若成绩在90分以上（包括90分）为“优”等，请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在等边三角形ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC=5，BD=4，有下列结论：①AE∥BC；②∠ADE=∠BDC；③△BDE是等边三角形；④△ADE的周长是9．其中，正确结论的个数是（ ）
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知在平面直角坐标系
中，直线
分别交
轴和
轴于点
.
(1)如图1，已知
经过点
，且与直线相切于点
，求的直径长；
(2)如图2，已知直线
分别交轴和轴于点
和点
，点
是直线
上的一个动点，以为圆心，
为半径画圆.
①当点与点重合时，求证: 直线与
相切；
②设与直线相交于
两点， 连结
. 问:是否存在这样的点，使得
是等腰直角三角形，若存在，求出点的坐标；若不存在，请说明理由.
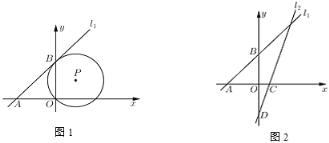
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解放桥是天津市的标志性建筑之一，是一座全钢结构的部分可开启的桥梁，
（I）如图①，已知解放桥可开启部分的桥面的跨度AB等于47m，从AB的中点C处开启，则AC开启至A'C'的位置时，A'C'的长为 .
（II）如图②，某校数学兴趣小组要测量解放桥的全长PQ，在观景平台M处测得∠PMQ=54°，沿河岸MQ前行，在观景平台N处测得∠PNQ=73°。已知PQ⊥MQ，MN=40m，求解放桥的全长PQ（tan54°≈1.4，tan73°≈3.3，结果保留整数）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
