
【题目】已知在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() .
.
(1)如图1,已知![]() 经过点
经过点![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]() ,求
,求![]() 的直径长;
的直径长;
(2)如图2,已知直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() 和点
和点![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点,以
上的一个动点,以![]() 为圆心,
为圆心,![]() 为半径画圆.
为半径画圆.
①当点![]() 与点
与点![]() 重合时,求证: 直线
重合时,求证: 直线![]() 与
与![]() 相切;
相切;
②设![]() 与直线
与直线![]() 相交于
相交于![]() 两点, 连结
两点, 连结![]() . 问:是否存在这样的点
. 问:是否存在这样的点![]() ,使得
,使得![]() 是等腰直角三角形,若存在,求出点
是等腰直角三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
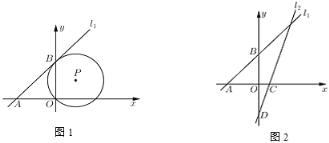
【答案】(1) ![]() 的直径长为
的直径长为![]() ;(2) ①见解析;②存在这样的点
;(2) ①见解析;②存在这样的点![]() 和
和![]() ,使得
,使得![]() 是等腰直角三角形.
是等腰直角三角形.
【解析】
(1)连接BC,证明△ABC为等腰直角三角形,则⊙P的直径长=BC=AB,即可求解;
(2)过点![]() 作
作![]() 于点
于点![]() ,证明CE=ACsin45°=4×
,证明CE=ACsin45°=4×![]() =2
=2![]() =圆的半径,即可求解;
=圆的半径,即可求解;
(3)假设存在这样的点![]() ,使得
,使得![]() 是等腰直角三角形,分点
是等腰直角三角形,分点![]() 在线段
在线段![]() 上时和点
上时和点![]() 在线段
在线段![]() 的延长线上两种情况,分别求解即可.
的延长线上两种情况,分别求解即可.
(1)如图3,连接BC,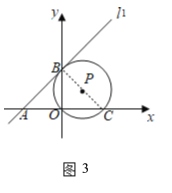
∵∠BOC=90°,
∴点P在BC上,
∵⊙P与直线l1相切于点B,
∴∠ABC=90°,而OA=OB,
∴△ABC为等腰直角三角形,
则⊙P的直径长=BC=AB=3![]()
(2)如图4过点![]() 作
作![]() 于点
于点![]() ,
,
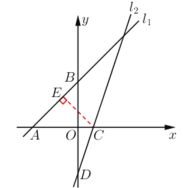
图4
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∵点![]() 与点
与点![]() 重合,
重合,
又![]() 的半径为
的半径为![]() ,
,
∴直线![]() 与
与![]() 相切.
相切.
②假设存在这样的点![]() ,使得
,使得![]() 是等腰直角三角形,
是等腰直角三角形,
∵直线![]() 经过点
经过点![]() ,
,
∴![]() 的函数解析式为
的函数解析式为![]() .
.
记直线![]() 与
与![]() 的交点为
的交点为![]() ,
,
情况一:
如图5,当点![]() 在线段
在线段![]() 上时,
上时,
由题意,得![]() .
.
如图,延长![]() 交
交![]() 轴于点
轴于点![]() ,
,
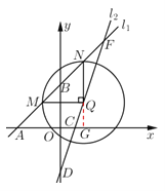
图5
∵![]() ,
,
∴![]() ,
,
即![]() 轴,
轴,
∴点![]() 与
与![]() 有相同的横坐标,
有相同的横坐标,
设![]() ,则
,则![]() ,
,
∴![]() .
.
∵![]() 的半径为
的半径为![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() ,
,
∴![]() 的坐标为
的坐标为![]() .
.
情况二:
当点![]() 在线段
在线段![]() 的延长线上时,同理可得
的延长线上时,同理可得![]() ,
,![]() 的坐标为
的坐标为![]() .
.
∴存在这样的点![]() 和
和![]() ,使得
,使得![]() 是等腰直角三角形.
是等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】拋物线![]() 分别交
分别交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .抛物线的对称轴
.抛物线的对称轴![]() 与
与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 与抛物线的对称轴
与抛物线的对称轴![]() 相交于点
相交于点![]() .
.
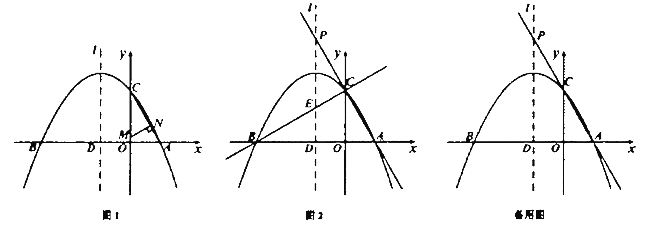
(1)直接写出抛物线的解折式和点![]() 的坐标;
的坐标;
(2)如图1,点![]() 为线段
为线段![]() 上的动点,点
上的动点,点![]() 为线段
为线段![]() 上的动点,且
上的动点,且![]() .在点
.在点![]() ,点
,点![]() 移动的过程中,
移动的过程中,![]() 是否有最小值?如果有,请求出最小值;
是否有最小值?如果有,请求出最小值;
(3)以点![]() 为旋转中心,将直线
为旋转中心,将直线![]() 绕点
绕点![]() 逆时针旋转,旋转角为
逆时针旋转,旋转角为![]() (
(![]() ),直线
),直线![]() 旋转时,与抛物线的对称轴
旋转时,与抛物线的对称轴![]() 相交于点
相交于点![]() ,与抛物线的另一个交点为点
,与抛物线的另一个交点为点![]() .
.
①如图2,当直线![]() 旋转到与直线
旋转到与直线![]() 重合时,判断线段
重合时,判断线段![]() 的数量关系?并说明理由
的数量关系?并说明理由
②当![]() 为等腰三角形时,请直按写出点
为等腰三角形时,请直按写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
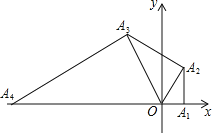
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以
,以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() ,再以
,再以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() ,再以
,再以![]() 为直角边作
为直角边作![]() ,并使
,并使![]() …按此规律进行下去,则点
…按此规律进行下去,则点![]() 的坐标为_______.
的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 经过等边
经过等边![]() 的顶点
的顶点![]() ,
,![]() (圆心
(圆心![]() 在
在![]() 内),分别与
内),分别与![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,
,![]() ,连结
,连结![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
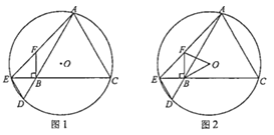
(1)求证:![]() .
.
(2)当![]() ,
,![]() 时,求
时,求![]() 的长。
的长。
(3)设![]() ,
,![]() .
.
①求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
②如图2,连结![]() ,
,![]() ,若
,若![]() 的面积是
的面积是![]() 面积的10倍,求
面积的10倍,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
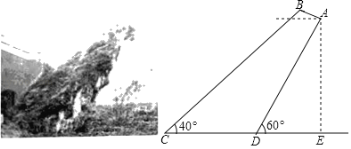
【题目】某地是国家AAAA级旅游景区,以“奇山奇水奇石景,古賨古洞古部落”享誉巴渠,被誉为 “小九寨”.端坐在观音崖旁的一块奇石似一只“啸天犬”,昂首向天,望穿古今.一个周末,某数学兴趣小组的几名同学想测出“啸天犬”上嘴尖与头顶的距离.他们把蹲着的“啸天犬”抽象成四边形ABCD,想法测出了尾部C看头顶B的仰角为![]() ,从前脚落地点D看上嘴尖A的仰角刚好
,从前脚落地点D看上嘴尖A的仰角刚好![]() ,
,![]() ,
,![]() .景区管理员告诉同学们,上嘴尖到地面的距离是
.景区管理员告诉同学们,上嘴尖到地面的距离是![]() .于是,他们很快就算出了AB的长.你也算算?(结果精确到
.于是,他们很快就算出了AB的长.你也算算?(结果精确到![]() .参考数据:
.参考数据:![]() .
.![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师提出问题:“一次函数的图象经过点A(3,2),B(-1,-6),由此可求得哪些结论?”小明思考后求得下列4个结论:①该函数表达式为y=2x-4;②该一次函数的函数值随自变量的增大而增大;③点P(2a,4a-4)在该函数图象上;④直线AB与坐标轴围成的三角形的面积为8.其中错误的结论是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
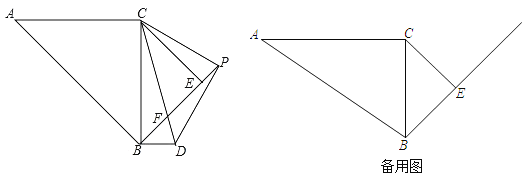
【题目】如图,在△ABC中,∠ACB=90°,tanA=![]() ,AC=6
,AC=6![]() ,以BC为斜边向右侧作等腰直角△EBC,P是BE延长线上一点,连接PC,以PC为直角边向下方作等腰直角△PCD,CD交线段BE于点F,连接BD.
,以BC为斜边向右侧作等腰直角△EBC,P是BE延长线上一点,连接PC,以PC为直角边向下方作等腰直角△PCD,CD交线段BE于点F,连接BD.
(1)求证:PC:CD=CE:BC;
(2)若PE=n(0<n≤4),求△BDP的面积;(用含n的代数式表示)
(3)当△BDF为等腰三角形时,请直接写出线段PE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com