
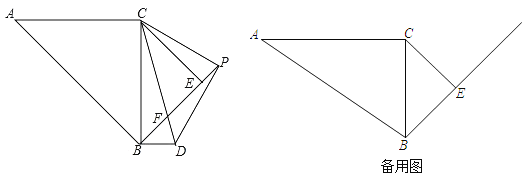
【题目】如图,在△ABC中,∠ACB=90°,tanA=![]() ,AC=6
,AC=6![]() ,以BC为斜边向右侧作等腰直角△EBC,P是BE延长线上一点,连接PC,以PC为直角边向下方作等腰直角△PCD,CD交线段BE于点F,连接BD.
,以BC为斜边向右侧作等腰直角△EBC,P是BE延长线上一点,连接PC,以PC为直角边向下方作等腰直角△PCD,CD交线段BE于点F,连接BD.
(1)求证:PC:CD=CE:BC;
(2)若PE=n(0<n≤4),求△BDP的面积;(用含n的代数式表示)
(3)当△BDF为等腰三角形时,请直接写出线段PE的长度.
【答案】(1)证明见解析;(2)S=2n2+![]() n(0<n≤4);(3)4
n(0<n≤4);(3)4![]() -4或4.
-4或4.
【解析】
(1)由△PCD,△EBC都是等腰直角三角形,得出CD=![]() PC,BC=
PC,BC=![]() CE,即可得出结论;
CE,即可得出结论;
(2)作PH⊥BD于H,首先利用四点共圆证明∠CBD=90°,再证明△CBD∽△CEP,求出BD、PH即可得出结果;
(3)分两种情形:①当BF=BD时,∠BDF=67.5°,在BC上取一点G,使得BG=BD,由BG+CG=BC构建方程即可得出结果;②当FB=FD时,∠FBD=∠FDB=45°,此时BD=BC=4![]() ,点E与点F重合,即可得出结果.
,点E与点F重合,即可得出结果.
(1)∵△PCD,△EBC都是等腰直角三角形,
∴CD=![]() PC,BC=
PC,BC=![]() CE,
CE,
∴![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ;
;
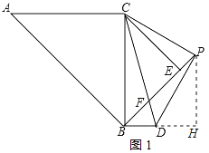
(2)如图1中,作PH⊥BD于H,
∵△PCD,△EBC都是等腰直角三角形,
∴∠PCD=∠BCE=45°,∠PBC=∠PDC=45°,
∴B、C、P、D四点共圆,
∴∠DBP=∠PCD=45°,
∴∠CBD=∠DBP+∠PBC=45°+45°=90°,△PBH是等腰直角三角形,
∵∠BCE=∠DCP=45°,
∴∠BCD=∠ECP,
∵∠CEP=∠CBD=90°,
∴△CBD∽△CEP,
∴![]() =
=![]() =
=![]() ,
,
∵PE=n,
∴BD=![]() n,
n,
∵tanA=![]() =
=![]() ,AC=6
,AC=6![]() ,
,
∴BC=4![]() ,
,
∴EC=BE=4,
∴PB=4+n,PH=BH=![]() (4+n),
(4+n),
∴S△BDP=![]() BDPH=
BDPH=![]() ×
×![]() n×
n×![]() (4+n)=2n2+
(4+n)=2n2+![]() n(0<n≤4);
n(0<n≤4);
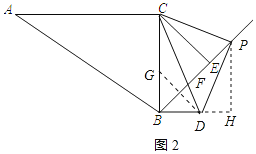
(3)①如图2中,当BF=BD时,在BC上取一点G,使得BG=BD,
∵∠PBD=45°,
∴∠BDF=67.5°,
∵∠CBD=90°,
∴∠BDG=∠BGD=45°,
∴∠BCD=∠GDC=22.5°,
∴GC=GD,
∵PE=n,BD=![]() n,
n,
∴BG=![]() n,CG=DG=
n,CG=DG=![]() BG=2n,
BG=2n,
∴BG+CG=BC=4![]() ,
,
∴![]() n+2n=4
n+2n=4![]() ,
,
∴n=4![]() -4,
-4,
∴PE=4![]() -4;
-4;
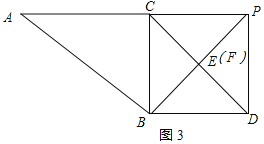
②如图3中,当FB=FD时,则∠FBD=∠FDB=45°,
此时BD=BC=4![]() ,
,
∵∠CDP=45°,
∴∠BDP=90°,
∵∠CPD=90°,∠CBD=90°,
∴四边形CBDP为正方形,E、F点重合,
∴PE=BE=4,
综上所述,线段PE的长度为:4![]() -4或4.
-4或4.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() .
.
(1)如图1,已知![]() 经过点
经过点![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]() ,求
,求![]() 的直径长;
的直径长;
(2)如图2,已知直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() 和点
和点![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点,以
上的一个动点,以![]() 为圆心,
为圆心,![]() 为半径画圆.
为半径画圆.
①当点![]() 与点
与点![]() 重合时,求证: 直线
重合时,求证: 直线![]() 与
与![]() 相切;
相切;
②设![]() 与直线
与直线![]() 相交于
相交于![]() 两点, 连结
两点, 连结![]() . 问:是否存在这样的点
. 问:是否存在这样的点![]() ,使得
,使得![]() 是等腰直角三角形,若存在,求出点
是等腰直角三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
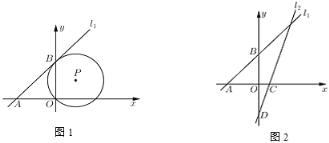
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁,
(I)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至A'C'的位置时,A'C'的长为 .
(II)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°。已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
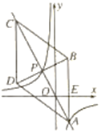
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数![]() 的图像相交于A,P两点。
的图像相交于A,P两点。
(1)求m,n的值与点A的坐标;
(2)求证:![]() ∽
∽![]()
(3)求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
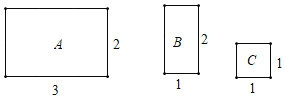
【题目】如图,A型、B型、C型三张矩形卡片的边长如图所示,将三张矩形卡片分别放入三个信封中,三个信封的外表完全相同;
(1)从这三个信封中随机抽取1个信封,则抽中A型矩形的概率为______;
(2)先从这三个信封中随机抽取1个信封(不放回),再从余下的两个信封中随机抽取1个信封,求事件“两次抽中的矩形卡片能拼成(无重叠无缝隙)一个新矩形”发生的概率.(列表法或树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
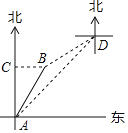
【题目】如图,南海某海域有两艘外国渔船A、B在小岛C的正南方向同一处捕鱼.一段时间后,渔船B沿北偏东30°的方向航行至小岛C的正东方向20海里处.
(1)求渔船B航行的距离;
(2)此时,在D处巡逻的中国渔政船同时发现了这两艘渔船,其中B渔船在点D的南偏西60°方向,A渔船在点D的西南方向,我渔政船要求这两艘渔船迅速离开中国海域.请分别求出中国渔政船此时到这两艘外国渔船的距离.(注:结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
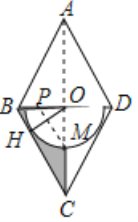
【题目】如图,在菱形ABCD中,连结BD、AC交于点O,过点O作![]() 于点H,以点O为圆心,OH为半径的半圆交AC于点M.
于点H,以点O为圆心,OH为半径的半圆交AC于点M.
①求证:DC是⊙O的切线.
②若![]() 且
且![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
③在②的条件下,P是线段BD上的一动点,当PD为何值时,![]() 的值最小,并求出最小值.
的值最小,并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).
(1)求该抛物线的解析式;
(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;
(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,G、F分别为AD、BC的中点,将纸片折叠,使D点落在GF上,得到△HAE,再过H点折叠纸片,使B点落在直线AB上,折痕为PQ.连接AF、EF,已知HE=HF,下列结论:①△MEH为等边三角形;②AE⊥EF;③△PHE∽△HAE;④ ![]() ,其中正确的结论是( )
,其中正确的结论是( )
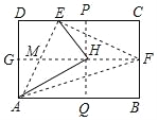
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com