
【题目】如图,矩形纸片ABCD中,G、F分别为AD、BC的中点,将纸片折叠,使D点落在GF上,得到△HAE,再过H点折叠纸片,使B点落在直线AB上,折痕为PQ.连接AF、EF,已知HE=HF,下列结论:①△MEH为等边三角形;②AE⊥EF;③△PHE∽△HAE;④ ![]() ,其中正确的结论是( )
,其中正确的结论是( )
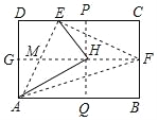
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【答案】D
【解析】试题解析:∵矩形纸片ABCD中,G、F分别为AD、BC的中点,
∴GF⊥AD,
由折叠可得,AH=AD=2AG,∠AHE=∠D=90°,
∴∠AHG=30°,∠EHM=90°-30°=60°,
∴∠HAG=60°=∠AED=∠MEH,
∴△EHM中,∠EMH=60°=∠EHM=∠MEH,
∴△MEH为等边三角形,故①正确;
∵∠EHM=60°,HE=HF,
∴∠HEF=30°,
∴∠FEM=60°+30°=90°,即AE⊥EF,故②正确;
∵∠PEH=∠MHE=60°=∠HEA,∠EPH=∠EHA=90°,
∴△PHE∽△HAE,故③正确;
设AD=2=AH,则AG=1,
∴Rt△AGH中,GH=![]() AG=
AG=![]() ,
,
Rt△AEH中,EH= ![]() ,
,
∴GF=![]() =AB,
=AB,
∴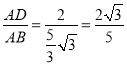 ,故④正确,
,故④正确,
综上所述,正确的结论是①②③④,
故选:D.


科目:初中数学 来源: 题型:
【题目】为了有效控制酒后驾车,某天黄石交警大队的一辆警车在东西方向的花湖大道上巡视,警车从某地A处出发,规定向东方向为正,当天行驶纪录如下(单位:千米)
+10,-9,+7,-15,+6,-5,+4,-2
(1)此时,这辆巡逻的汽车司机如何向队长描述他的位置?
(2)如果警车行驶1千米耗油0.2升,油箱有油10升,现在警车要回到出发点A处,那么油箱的油够不够?若不够,途中至少需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)猜想与计算:
邻边长分别为3和5的平行四边形是_______阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD___________阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一蓄水池有漏水现象,如果用一台水泵向该水池注水,需用8小时才能将空水池注满,如果用同样的两台水泵向该水池注水,只需3.2小时就能将空池注满,如要求2小时内就将该水池注满,至少需要几台这样的水泵?
查看答案和解析>>
科目:初中数学 来源: 题型:
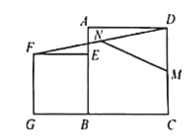
【题目】如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F分别是平行四边形ABCD的边BC、AD上的点,且BE=DF.
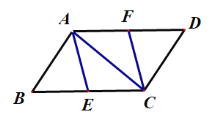
(1)求证:四边形AECF为平行四边形;
(2)若AE=BE,∠BAC=90°,判断四边形AECF的形状并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨) | 水价(元/吨) |
第一级 20吨以下(含20吨) | 1.6 |
第二级 20吨﹣30吨(含30吨) | 2.4 |
第三级 30吨以上 | 3.2 |
例:某用户的月用水量为32吨,按三级计量应缴水费为:
1.6×20+2.4×10+3.2×2=62.4(元)
(1)如果甲用户的月用水量为12吨,则甲需缴的水费为 元;
(2)如果乙用户缴的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为a吨,则丙用户该月应缴水费多少元?(用含a的代数式表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com