
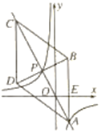
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数![]() 的图像相交于A,P两点。
的图像相交于A,P两点。
(1)求m,n的值与点A的坐标;
(2)求证:![]() ∽
∽![]()
(3)求![]() 的值
的值
【答案】(1)![]() ,
,![]() ,
,![]() 点的坐标是
点的坐标是![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)根据点P的坐标,利用待定系数法可求出m,n的值,利用正、反比例函数图象的对称性结合点P的坐标找出点A的坐标即可解答;
(2)由菱形的性质可得出AC⊥BD,AB∥CD,利用平行线的性质可得出∠DCP=∠OAE,结合AB⊥x轴可得出∠AEO=∠CPD=90°,进而即可证出△CPD∽△AEO;
(3)由点A的坐标可得出AE,OE,AO的长,由相似三角形的性质可得出∠CDP=∠AOE,再利用正弦的定义即可求出sin∠CDB的值.
解:(1)∵正比例函数![]() ,反比例函数
,反比例函数![]() 均经过点
均经过点![]() ,
,
∴![]() ,
,![]() ,
,
解得:![]() ,
,![]() .
.
∴正比例函数![]() ,反比例函数
,反比例函数![]() .
.
又正比例函数与反比例函数均是中心对称图形,则其两个交点也成中心对称点,
∵![]() ,
,
∴![]() 点的坐标是
点的坐标是![]() .
.
(2)证明:∵四边形ABCD是菱形,
∴AC⊥BD,AB∥CD,
∴∠DCP=∠BAP,即∠DCP=∠OAE.
∵AB⊥x轴,
∴∠AEO=∠CPD=90°,
∴△CPD∽△AEO.
(3)∵![]() 点的坐标是
点的坐标是![]() .
.
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴△CPD∽△AEO,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成如下统计图表.
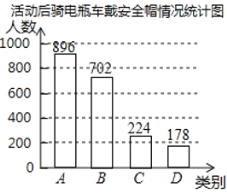

活动前骑电瓶车戴安全帽情况统计表
类别 | 人数 |
| 68 |
| 245 |
| 510 |
| 177 |
合计 | 1000 |
(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;
(3)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是( )
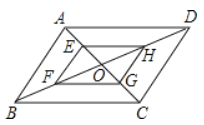
A.EH=HGB.四边形EFGH是平行四边形
C.AC⊥BDD.![]() 的面积是
的面积是![]() 的面积的2倍
的面积的2倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校为了让学生的课余生活丰富多彩,开展了以下课外活动:
代号 | 活动类型 |
A | 经典诵读与写作 |
B | 数学兴趣与培优 |
C | 英语阅读与写作 |
D | 艺体类 |
E | 其他 |
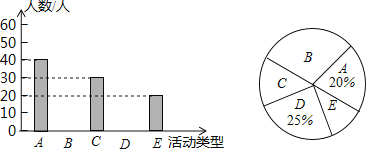
为了解学生的选择情况,现从该校随机抽取了部分学生进行问卷调查(参与问卷调查的每名学生只能选择其中一项),并根据调查得到的数据绘制了如图所示的两幅不完整的统计图.请根据统计图提供的信息回答下列问题(要求写出简要的解答过程).
(1)此次共调查了 名学生.
(2)将条形统计图补充完整.
(3)“数学兴趣与培优”所在扇形的圆心角的度数为 .
(4)若该校共有2000名学生,请估计该校喜欢A、B、C三类活动的学生共有多少人?
(5)学校将从喜欢“A”类活动的学生中选取4位同学(其中女生2名,男生2名)参加校园“金话筒”朗诵初赛,并最终确定两名同学参加决赛,请用列表或画树状图的方法,求出刚好一男一女参加决赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
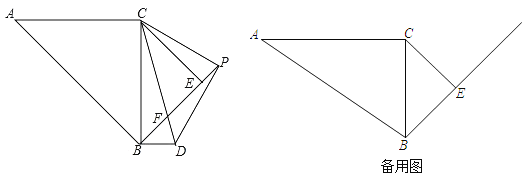
【题目】如图,在△ABC中,∠ACB=90°,tanA=![]() ,AC=6
,AC=6![]() ,以BC为斜边向右侧作等腰直角△EBC,P是BE延长线上一点,连接PC,以PC为直角边向下方作等腰直角△PCD,CD交线段BE于点F,连接BD.
,以BC为斜边向右侧作等腰直角△EBC,P是BE延长线上一点,连接PC,以PC为直角边向下方作等腰直角△PCD,CD交线段BE于点F,连接BD.
(1)求证:PC:CD=CE:BC;
(2)若PE=n(0<n≤4),求△BDP的面积;(用含n的代数式表示)
(3)当△BDF为等腰三角形时,请直接写出线段PE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
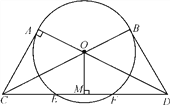
【题目】如图,过⊙O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交⊙O于点E、F,过圆心O作OM⊥CD,垂足为M点.
(1)判断△COD的形状并说明理由;
(2)若CE=3,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,与
,与![]() 轴相交于
轴相交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 右侧),与
右侧),与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式和![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)如图1,若点![]() 是抛物线上
是抛物线上![]() 、
、![]() 两点之间的一个动点(不与
两点之间的一个动点(不与![]() 、
、![]() 重合),是否存在点
重合),是否存在点![]() ,使四边形
,使四边形![]() 的面积最大?若存在,求点
的面积最大?若存在,求点![]() 的坐标及四边形
的坐标及四边形![]() 面积的最大值;若不存在,请说明理由;
面积的最大值;若不存在,请说明理由;
(3)如图2,若点![]() 是抛物线上任意一点,过点
是抛物线上任意一点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com