
【题目】已知抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,与
,与![]() 轴相交于
轴相交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 右侧),与
右侧),与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的解析式和![]() ,
,![]() 两点的坐标;
两点的坐标;
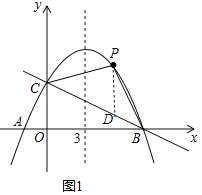
(2)如图1,若点![]() 是抛物线上
是抛物线上![]() 、
、![]() 两点之间的一个动点(不与
两点之间的一个动点(不与![]() 、
、![]() 重合),是否存在点
重合),是否存在点![]() ,使四边形
,使四边形![]() 的面积最大?若存在,求点
的面积最大?若存在,求点![]() 的坐标及四边形
的坐标及四边形![]() 面积的最大值;若不存在,请说明理由;
面积的最大值;若不存在,请说明理由;
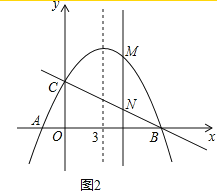
(3)如图2,若点![]() 是抛物线上任意一点,过点
是抛物线上任意一点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)存在点
;(2)存在点![]() ,使四边形
,使四边形![]() 的面积最大;点
的面积最大;点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 面积的最大值为32;(3)点
面积的最大值为32;(3)点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
(1)由抛物线的对称轴是直线 x=3,解出 a的值,即可求得抛物线解析式,在
令其 y值为零,解一元二次方程即可求出 A和 B的坐标;
(2)易求点 C的坐标为(0,4),设直线 BC的解析式为 y=kx+b(k≠0),将 B(8,0),
C(0,4)代入 y=kx+b,解出 k和 b的值,即得直线 BC的解析式;设点 P的坐标为![]() ,过点 P作 PD∥y轴,交直线 BC于点 D,则点 D的坐标为
,过点 P作 PD∥y轴,交直线 BC于点 D,则点 D的坐标为![]() , 利用关系式 S四边形 PBOC=S△BOC+S△PBC得出关于 x的二次函数,从而求得其最值;
, 利用关系式 S四边形 PBOC=S△BOC+S△PBC得出关于 x的二次函数,从而求得其最值;
(3)设点 M的坐标为![]() 则点 N的坐标为
则点 N的坐标为![]() ,
,![]() ,分当 0<m<8时,或当 m<0或 m> 8时来化简绝对值,从而求解.
,分当 0<m<8时,或当 m<0或 m> 8时来化简绝对值,从而求解.
(1)![]() 抛物线的对称轴是直线
抛物线的对称轴是直线![]() ,
,
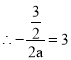 ,解得
,解得![]() ,
,
![]()
![]() 抛物线的解析式为:
抛物线的解析式为:![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
答:抛物线的解析式为:![]() ;点
;点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(2)当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]() 代入
代入![]() 得
得
![]() ,解得
,解得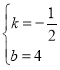 ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
假设存在点![]() ,使四边形
,使四边形![]() 的面积最大,
的面积最大,
设点![]() 的坐标为
的坐标为![]() ,如图所示,过点
,如图所示,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
则![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 时,四边形
时,四边形![]() 的面积最大,最大值是32
的面积最大,最大值是32
![]() ,
,
![]() 存在点
存在点![]() ,使得四边形
,使得四边形![]() 的面积最大.
的面积最大.
答:存在点![]() ,使四边形
,使四边形![]() 的面积最大;点
的面积最大;点![]() 的坐标为
的坐标为![]() ,四边形
,四边形![]() 面积的最大值为32.
面积的最大值为32.
(3)设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
当![]() 或
或![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
答:点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
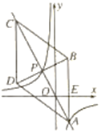
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数![]() 的图像相交于A,P两点。
的图像相交于A,P两点。
(1)求m,n的值与点A的坐标;
(2)求证:![]() ∽
∽![]()
(3)求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).
(1)求该抛物线的解析式;
(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;
(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
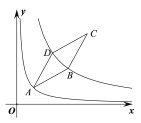
【题目】如图,菱形ABCD顶点A在例函数y=![]() (x>0)的图象上,函数 y=
(x>0)的图象上,函数 y=![]() (k>3,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=2,∠DAB=30°,则k的值为______.
(k>3,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=2,∠DAB=30°,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
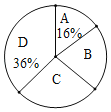
【题目】为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
(1)本次调查一共随机抽取了 个参赛学生的成绩;
(2)表1中![]() ;
;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有 人.
表1 知识竞赛成绩分组统计表
组别 | 分数/分 | 频数 |
A |
| a |
B |
| 10 |
C |
| 14 |
D |
| 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
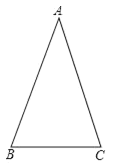
【题目】如图,△ABC中,AB=AC,∠A=36°.
(1)用尺规作图作∠ABC的角平分线,交AC于点D;(保留作图痕迹,不写作法).
(2)求证:△BCD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,G、F分别为AD、BC的中点,将纸片折叠,使D点落在GF上,得到△HAE,再过H点折叠纸片,使B点落在直线AB上,折痕为PQ.连接AF、EF,已知HE=HF,下列结论:①△MEH为等边三角形;②AE⊥EF;③△PHE∽△HAE;④ ![]() ,其中正确的结论是( )
,其中正确的结论是( )
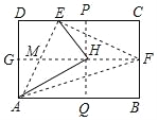
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于A,B两点,交y轴于点C.直线
交x轴于A,B两点,交y轴于点C.直线![]() 经过点A,C.
经过点A,C.
(1)求抛物线的解析式;
(2)点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.
①当![]() 是直角三角形时,求点P的坐标;
是直角三角形时,求点P的坐标;
②作点B关于点C的对称点![]() ,则平面内存在直线l,使点M,B,
,则平面内存在直线l,使点M,B,![]() 到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线
到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线![]() 的解析式.(k,b可用含m的式子表示)
的解析式.(k,b可用含m的式子表示)
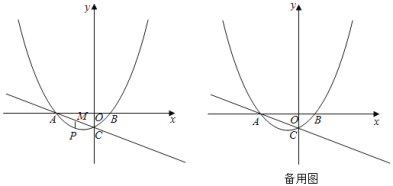
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学课题研究小组针对兰州市住房窗户“如何设计遮阳篷”这一课题进行了探究,过程如下:
问题提出:
如下图是某住户窗户上方安装的遮阳蓬,要求设计的遮阳篷既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.

方案设计:
如下图,该数学课题研究小组通过调查研究设计了垂直于墙面![]() 的遮阳篷
的遮阳篷![]()
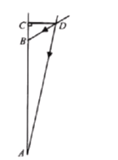
数据收集:
通过查阅相关资料和实际测量:兰州市一年中,夏至这一天的正午时刻,太阳光线![]() 与遮阳篷
与遮阳篷![]() 的夹角
的夹角![]() 最大(
最大(![]() ):冬至这一天的正午时刻,太阳光线
):冬至这一天的正午时刻,太阳光线![]() 与遮阳篷
与遮阳篷![]() 的夹角
的夹角![]() 最小(
最小(![]() );窗户的高度
);窗户的高度![]()
问题解决:
根据上述方案及数据,求遮阳篷![]() 的长.(结果精确到
的长.(结果精确到![]() ,参考数据:
,参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com