
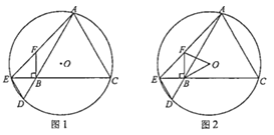
【题目】如图1,![]() 经过等边
经过等边![]() 的顶点
的顶点![]() ,
,![]() (圆心
(圆心![]() 在
在![]() 内),分别与
内),分别与![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,
,![]() ,连结
,连结![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)当![]() ,
,![]() 时,求
时,求![]() 的长。
的长。
(3)设![]() ,
,![]() .
.
①求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
②如图2,连结![]() ,
,![]() ,若
,若![]() 的面积是
的面积是![]() 面积的10倍,求
面积的10倍,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() ;(3)①
;(3)①![]() ; ②
; ②![]() 或
或![]() .
.
【解析】
(1)根据等边三角形的性质和圆周角定理解答即可;
(2)过点A作AG⊥BC于点G,根据等边三角形的性质和勾股定理解得即可;
(3)①过点E作EH⊥AD于点H,根据三角函数和函数解析式解得即可;
②过点O作OM⊥BC于点M,根据相似三角形的判定和性质解答即可.
(1)证明:∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
(2)解:如图,过点![]() 作
作![]() 于点
于点![]() .
.
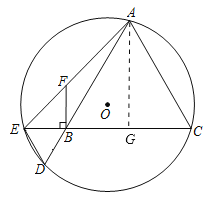
∵![]() 为等边三角形,
为等边三角形,![]() ,
,
∴![]() .
.
∴在![]() 中,
中,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴在![]() 中,
中,![]() .
.
(3)解:①如图,过点![]() 作
作![]() 于点
于点![]() .
.
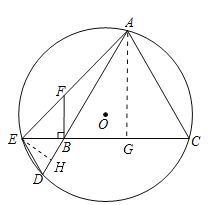
∵![]() ,
,
∴在![]() 中,
中,![]() .
.
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() .
.
∴![]() .
.
∴![]() .
.
∴在![]() 中,
中,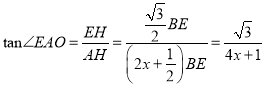 .
.
![]() .
.
②如图,过点![]() 作
作![]() 于点
于点![]() .
.
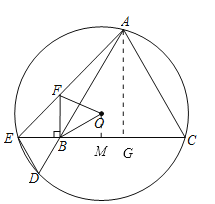
设![]() .
.
∵![]() ,
,
∴![]() ./p>
./p>
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() .
.
∴![]() ,
,
∴![]() 的面积
的面积![]() ,
,
∴![]() 的面积
的面积![]() .
.
∵![]() 的面积是
的面积是![]() 的面积10倍,
的面积10倍,
∴![]() ,
,
∴![]() .
.
解得![]() ,
,![]() .
.
∴![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图是某品牌太阳能热水器的侧面示意图.已知铁架水平横管![]() 平行于水平线AD,长为
平行于水平线AD,长为![]() 的真空管
的真空管![]() 与水平线
与水平线![]() 的夹角为37°,铁架
的夹角为37°,铁架![]() 的倾斜角
的倾斜角![]() 为22°,铁架竖直管
为22°,铁架竖直管![]() 的长度为05
的长度为05 ![]() ,根据以上信息,请求出:
,根据以上信息,请求出:

(1))真空管上端![]() 到水平线
到水平线![]() 的距离;
的距离;
(2)水平横管![]() 的长度(结果精确到0.1
的长度(结果精确到0.1 ![]() )(参考数据:
)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
成绩x(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,有下列结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△ADE的周长是9.其中,正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
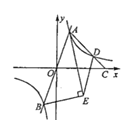
【题目】如图,过原点的直线与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,点
两点,点![]() 在第一象限点
在第一象限点![]() 在
在![]() 轴正半轴上,连结
轴正半轴上,连结![]() 交反比例函数图象于点
交反比例函数图象于点![]() .
.![]() 为
为![]() 的平分线,过点
的平分线,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连结
,连结![]() .若
.若![]() ,
,![]() 的面积为8,则
的面积为8,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() .
.
(1)如图1,已知![]() 经过点
经过点![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]() ,求
,求![]() 的直径长;
的直径长;
(2)如图2,已知直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() 和点
和点![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点,以
上的一个动点,以![]() 为圆心,
为圆心,![]() 为半径画圆.
为半径画圆.
①当点![]() 与点
与点![]() 重合时,求证: 直线
重合时,求证: 直线![]() 与
与![]() 相切;
相切;
②设![]() 与直线
与直线![]() 相交于
相交于![]() 两点, 连结
两点, 连结![]() . 问:是否存在这样的点
. 问:是否存在这样的点![]() ,使得
,使得![]() 是等腰直角三角形,若存在,求出点
是等腰直角三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
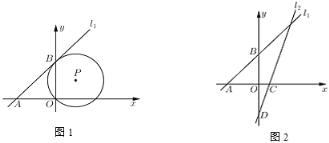
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 过点
过点![]() .
.
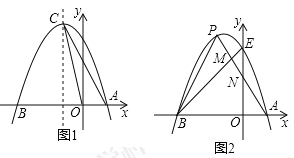
(1)求抛物线的解析式及其顶点C的坐标;
(2)设点D是x轴上一点,当![]() 时,求点D的坐标;
时,求点D的坐标;
(3)如图2.抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N,![]() 和
和![]() 的面积分别为
的面积分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.
(1)若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?
(2)若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
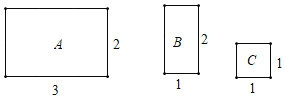
【题目】如图,A型、B型、C型三张矩形卡片的边长如图所示,将三张矩形卡片分别放入三个信封中,三个信封的外表完全相同;
(1)从这三个信封中随机抽取1个信封,则抽中A型矩形的概率为______;
(2)先从这三个信封中随机抽取1个信封(不放回),再从余下的两个信封中随机抽取1个信封,求事件“两次抽中的矩形卡片能拼成(无重叠无缝隙)一个新矩形”发生的概率.(列表法或树状图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com