
【题目】拋物线![]() 分别交
分别交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .抛物线的对称轴
.抛物线的对称轴![]() 与
与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 与抛物线的对称轴
与抛物线的对称轴![]() 相交于点
相交于点![]() .
.
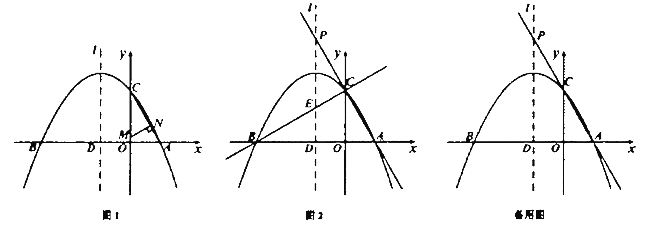
(1)直接写出抛物线的解折式和点![]() 的坐标;
的坐标;
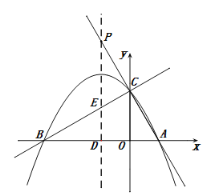
(2)如图1,点![]() 为线段
为线段![]() 上的动点,点
上的动点,点![]() 为线段
为线段![]() 上的动点,且
上的动点,且![]() .在点
.在点![]() ,点
,点![]() 移动的过程中,
移动的过程中,![]() 是否有最小值?如果有,请求出最小值;
是否有最小值?如果有,请求出最小值;
(3)以点![]() 为旋转中心,将直线
为旋转中心,将直线![]() 绕点
绕点![]() 逆时针旋转,旋转角为
逆时针旋转,旋转角为![]() (
(![]() ),直线
),直线![]() 旋转时,与抛物线的对称轴
旋转时,与抛物线的对称轴![]() 相交于点
相交于点![]() ,与抛物线的另一个交点为点
,与抛物线的另一个交点为点![]() .
.
①如图2,当直线![]() 旋转到与直线
旋转到与直线![]() 重合时,判断线段
重合时,判断线段![]() 的数量关系?并说明理由
的数量关系?并说明理由
②当![]() 为等腰三角形时,请直按写出点
为等腰三角形时,请直按写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)有最小值,
;(2)有最小值,![]() ;(3)①
;(3)①![]() ,见解析;②
,见解析;②![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
【解析】
⑴用待定系数法可得抛物线的解析式为:![]() ; 根据对称轴求法
; 根据对称轴求法![]() ,可得
,可得![]() .
.
⑵根据三角函数即可解得;
⑶①设直线![]() 的解析式为
的解析式为![]() ,由待定系数法可得直线
,由待定系数法可得直线![]() 的解析式为,再根据三角函数即可得到答案;
的解析式为,再根据三角函数即可得到答案;
②根据等腰三角形的性质即可得到答案.
解:⑴因为拋物线![]() 分别交
分别交![]() 轴于点
轴于点![]() ,用待定系数法可得
,用待定系数法可得
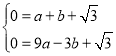 ,解得
,解得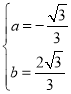 抛物线的解析式为:
抛物线的解析式为:![]() ;
;
由抛物线的对称轴![]() 与
与![]() 轴相交于点
轴相交于点![]() ,根据对称轴求法
,根据对称轴求法![]() ,可得
,可得![]() .
.
⑵在![]() 移动的过程中,
移动的过程中,![]() 有最小值.
有最小值.
∵![]()
∴在![]() 中,
中,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
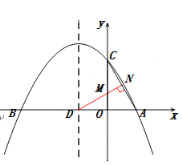
根据垂线段最短,![]() 的长就是
的长就是![]() 的最小值.
的最小值.
∵![]() ,
,![]() ,∴
,∴![]()
∴在![]() 中,
中,![]() .
.
⑶①![]()
理由如下:设直线![]() 的解析式为
的解析式为![]()
将![]() ,
,![]() 代入
代入![]()
于是得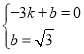 ,解得
,解得 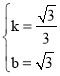
∴直线![]() 的解析式为
的解析式为![]() ,
,
∵点![]() ,∴点
,∴点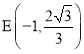 ,∴
,∴![]()
∵![]() ,∴
,∴![]()
∴在![]() 中,由⑵得,
中,由⑵得,![]()
∴![]() ,∴
,∴![]() ,
,
∴![]()
∴![]() .
.
②当![]() 为等腰三角形时点
为等腰三角形时点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
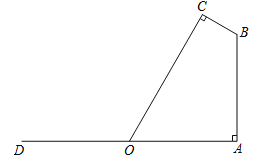
【题目】如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+6x﹣5与x轴交于A,B两点(点A在点B左边),与y轴交于点C.点P是抛物线上一个动点,过点P作x轴的垂线,垂足为点H,交直线BC于点E.
(1)求点A,B,C的坐标;
(2)连接CP,当CP平分∠OCB时,求点P的坐标;
(3)平面直角坐标系内是否存在点Q,使得以点P,E,B,Q为顶点的四边形为菱形?若存在,直接写出点Q的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.
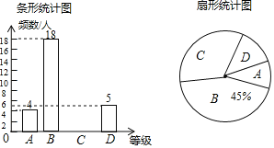
(1)本次一共抽取了几名九年级学生?
(2)补全条形统计图;
(3)在扇形统计图中,C对应的扇形的圆心角是几度?
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌太阳能热水器的侧面示意图.已知铁架水平横管![]() 平行于水平线AD,长为
平行于水平线AD,长为![]() 的真空管
的真空管![]() 与水平线
与水平线![]() 的夹角为37°,铁架
的夹角为37°,铁架![]() 的倾斜角
的倾斜角![]() 为22°,铁架竖直管
为22°,铁架竖直管![]() 的长度为05
的长度为05 ![]() ,根据以上信息,请求出:
,根据以上信息,请求出:

(1))真空管上端![]() 到水平线
到水平线![]() 的距离;
的距离;
(2)水平横管![]() 的长度(结果精确到0.1
的长度(结果精确到0.1 ![]() )(参考数据:
)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
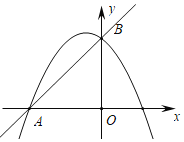
(3)如图,当![]() 时,在抛物线上是否存在点
时,在抛物线上是否存在点![]() ,使
,使![]() 的面积为1?若存在,请求出符合条件的所有点
的面积为1?若存在,请求出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
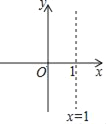
【题目】在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c).
(1)当c=﹣3时,点(x1,y1)在抛物线y=x2﹣2x+c上,求y1的最小值;
(2)若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA=![]() OB,求抛物线的解析式;
OB,求抛物线的解析式;
(3)当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)方法选择
如图①,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() ,
,![]() .求证:
.求证:![]() .
.
小颖认为可用截长法证明:在![]() 上截取
上截取![]() ,连接
,连接![]() …
…
小军认为可用补短法证明:延长![]() 至点
至点![]() ,使得
,使得![]() …
…
请你选择一种方法证明.
(2)类比探究
(探究1)
如图②,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() .试用等式表示线段
.试用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
(探究2)
如图③,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的直径,
的直径,![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 之间的等量关系式是______.
之间的等量关系式是______.
(3)拓展猜想
如图④,四边形![]() 是
是![]() 的内接四边形,连接
的内接四边形,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的直径,
的直径,![]() ,则线段
,则线段![]() ,
,![]() ,
,![]() 之间的等量关系式是______.
之间的等量关系式是______.
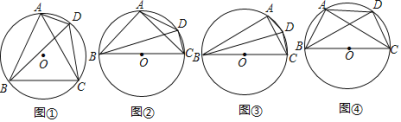
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() .
.
(1)如图1,已知![]() 经过点
经过点![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]() ,求
,求![]() 的直径长;
的直径长;
(2)如图2,已知直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() 和点
和点![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点,以
上的一个动点,以![]() 为圆心,
为圆心,![]() 为半径画圆.
为半径画圆.
①当点![]() 与点
与点![]() 重合时,求证: 直线
重合时,求证: 直线![]() 与
与![]() 相切;
相切;
②设![]() 与直线
与直线![]() 相交于
相交于![]() 两点, 连结
两点, 连结![]() . 问:是否存在这样的点
. 问:是否存在这样的点![]() ,使得
,使得![]() 是等腰直角三角形,若存在,求出点
是等腰直角三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
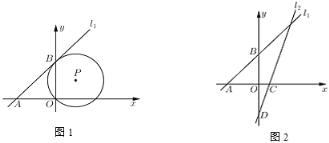
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com