
【题目】数学课上,老师提出问题:“一次函数的图象经过点A(3,2),B(-1,-6),由此可求得哪些结论?”小明思考后求得下列4个结论:①该函数表达式为y=2x-4;②该一次函数的函数值随自变量的增大而增大;③点P(2a,4a-4)在该函数图象上;④直线AB与坐标轴围成的三角形的面积为8.其中错误的结论是( )
A. ①B. ②C. ③D. ④
【答案】D
【解析】
(1)根据两点坐标,代入y=kx+b,求出一次函数表达式。(2)根据一次函数表达式,判断一次函数随自变量的增大而增大。(3)把点P(2a,4a-4)代入一次函数表达式。(4)求出A、B点的坐标然后利用三角形面积公式求出.
①设所求的直线解析式为y=kx+b,
∵ 一次函数的图象经过点A(3,2),B(-1,-6),
∴,3k+b=2 -k+b=-6
解得 k=2 b=-4
∴ 该函数表达式为y=2x-4; 故①正确;
② ∵k=2>0,
∴ 该一次函数的函数值随自变量的增大而增大; 故②正确;
③ 把x=2a代入y=2x-4,得y=4a-4,
∴点P(2a,4a-4)在该函数图象上,故③正确;
④ 把x=0,代入y=2x-4,得y=-4,
∴该函数与y轴的交点坐标为(0,-4);
把y=0,代入y=2x-4,得x=2,
∴该函数与x轴的交点坐标为(2,0);
∴ 直线AB与坐标轴围成的三角形的面积为=![]() ×2×4=4∴④错误.
×2×4=4∴④错误.
故答案为: D.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
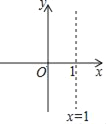
【题目】在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c).
(1)当c=﹣3时,点(x1,y1)在抛物线y=x2﹣2x+c上,求y1的最小值;
(2)若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA=![]() OB,求抛物线的解析式;
OB,求抛物线的解析式;
(3)当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,有下列结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△ADE的周长是9.其中,正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() .
.
(1)如图1,已知![]() 经过点
经过点![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]() ,求
,求![]() 的直径长;
的直径长;
(2)如图2,已知直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() 和点
和点![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点,以
上的一个动点,以![]() 为圆心,
为圆心,![]() 为半径画圆.
为半径画圆.
①当点![]() 与点
与点![]() 重合时,求证: 直线
重合时,求证: 直线![]() 与
与![]() 相切;
相切;
②设![]() 与直线
与直线![]() 相交于
相交于![]() 两点, 连结
两点, 连结![]() . 问:是否存在这样的点
. 问:是否存在这样的点![]() ,使得
,使得![]() 是等腰直角三角形,若存在,求出点
是等腰直角三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
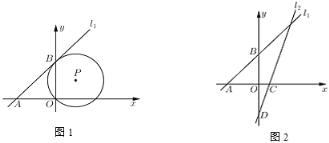
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 过点
过点![]() .
.
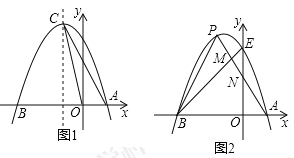
(1)求抛物线的解析式及其顶点C的坐标;
(2)设点D是x轴上一点,当![]() 时,求点D的坐标;
时,求点D的坐标;
(3)如图2.抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N,![]() 和
和![]() 的面积分别为
的面积分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级共有360名学生.为了解该校九年级学生每周运动的时间,从中随机抽取了若干名学生进行问卷调查,并将获得的数据(每周运动的时间,单位:小时)进行整理、描述和分析.下面给出了部分信息.
I.学生每周运动的时间的频数分布直方图如下(数据分成6组:1≤x<3,3≤x<5,5≤x<7,7≤x<9,9≤x<11,11≤x≤13)
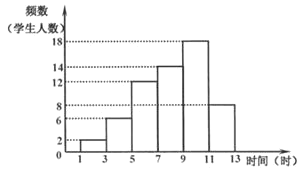
Ⅱ.学生每周运动的时间在7≤x<9这一组的数据是:
7,7.2,7.4,7.5,7.5,7.6,7.8,7.8,8,8.2,8.4,8.5,8.6,8.8根据以上信息,解答下列问题:
(1)求这次被抽取的学生数。
(2)写出被抽取学生每周运动的时间的中位数.
(3)根据此次问卷调查结果,估计该校九年级全体学生每周运动的时间超过7.9小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.
(1)若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?
(2)若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放桥是天津市的标志性建筑之一,是一座全钢结构的部分可开启的桥梁,
(I)如图①,已知解放桥可开启部分的桥面的跨度AB等于47m,从AB的中点C处开启,则AC开启至A'C'的位置时,A'C'的长为 .
(II)如图②,某校数学兴趣小组要测量解放桥的全长PQ,在观景平台M处测得∠PMQ=54°,沿河岸MQ前行,在观景平台N处测得∠PNQ=73°。已知PQ⊥MQ,MN=40m,求解放桥的全长PQ(tan54°≈1.4,tan73°≈3.3,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
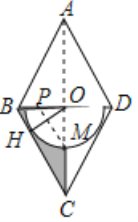
【题目】如图,在菱形ABCD中,连结BD、AC交于点O,过点O作![]() 于点H,以点O为圆心,OH为半径的半圆交AC于点M.
于点H,以点O为圆心,OH为半径的半圆交AC于点M.
①求证:DC是⊙O的切线.
②若![]() 且
且![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
③在②的条件下,P是线段BD上的一动点,当PD为何值时,![]() 的值最小,并求出最小值.
的值最小,并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com