
����Ŀ������ͨѶ����Ѹ�ͷ�չ��������֮��Ĺ�ͨ��ʽ����������ݣ�ijУ��ѧ��ȤС�������������ϲ���Ĺ�ͨ��ʽ�������ʾ�(ÿ�˱�ѡ��ֻѡһ��)����ȫУ��Χ����������˲���ѧ������ͳ�ƽ������������������������ͳ��ͼ������ͼ����������Ϣ����������⣺

(1)���ͳ�ƹ������_____��ѧ������ϲ���õ绰��ͨ������Ӧ���ε�Բ�Ľ���____����
(2)������ͳ��ͼ����������
(3)������εĵ���������1200��ѧ������ϲ����QQ���й�ͨ��ѧ���ж�������
(4)�ס�������ͬѧ���ţ�QQ���绰���ֹ�ͨ��ʽ�����ѡ��һ�ַ�ʽ��Է���ϵ�������б�����״ͼ�ķ��������������ͬѧǡ��ѡ��ͬһ�ֹ�ͨ��ʽ�ĸ��ʣ�
���𰸡�(1)120��54��(2)��ͼ��������(3)660����(4)![]() .
.
��������
(1)��ϲ��ʹ���ŵ�������������ռ�İٷֱȵõ������������������360�����������е绰������ռ������
(2)�ȼ����ϲ��ʹ�ö��ŵ�������Ȼ��ȫ����ͳ��ͼ��
(3)���������������壬��1200������������ϲ����QQ���й�ͨ��ѧ����ռ�İٷֱȼ��ɣ�
(4)����״ͼչʾ����9�ֵȿ��ܵĽ���������ҳ���������ͬѧǡ��ѡ��ͬһ�ֹ�ͨ��ʽ�Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
�⣺(1)���ͳ�ƹ����ѧ��24��20%��120(��)��������ϲ���õ绰��ͨ������Ӧ���ε�Բ�Ľ���360���![]() ��54����
��54����
�ʴ�Ϊ��120��54��
(2)ϲ��ʹ�ö��ŵ�����Ϊ120��18��24��66��2��10(��)��
����ͳ��ͼΪ��
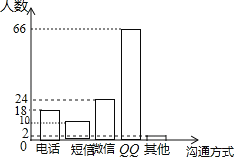
(3)1200��![]() ��660��
��660��
���Թ���1200��ѧ������ϲ����QQ���й�ͨ��ѧ����660����
(4)����״ͼΪ��

����9�ֵȿ��ܵĽ��������������ͬѧǡ��ѡ��ͬһ�ֹ�ͨ��ʽ�Ľ����Ϊ3��
���Լ�������ͬѧǡ��ѡ��ͬһ�ֹ�ͨ��ʽ�ĸ���![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪A(3��0),B(0��-1)������AB,��B����AB�Ĵ��߶�,ʹBA=BC,����AC.
(1)��ͼ1����C�����ꣻ
(2)��ͼ2,��P���A�����,��x������ƽ��,����BP,������ֱ����������BPQ,����CQ.��֤:PA=CQ.
(3)��(2)��������,��C��P��Q���㹲��,���ʱP�����꼰��APB�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ϣ������Ѹ�ͷ�չ������ȥ�̳������֧����ʽ���Ӷ�������ݣ�ijУ��ѧ��ȤС�������һ�ݵ����ʾ���Ҫ��ÿ��ѡ��ֻѡһ������ϲ����֧����ʽ���ֽ�����������ͳ�Ʋ����Ƴ�����������������ͳ��ͼ������ͼ����������Ϣ����������⣺
��1����λ���������� ���ˣ�������ͳ��ͼ�У���ʾ��֧������֧��������Բ�ĽǵĶ���Ϊ�� ����
��2��������ͳ��ͼ�����������۲��ͼ��֧����ʽ���������������� ������
��3����һ�ι����У�С����С�����������������֧�������������п�������֧����ʽ��ѡһ�ַ�ʽ����֧�������û���״ͼ���б���ķ������������ǡ��ѡ��ͬһ��֧����ʽ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�ı�OA��OC�ֱ���x�ᣬy���ϣ�OC��7����B�ڵ�һ���ޣ���D�ڱ�AB�ϣ���E�ڱ�BC�ϣ��ҡ�BDE��30�㣬����BDE��DE�۵��õ���B��DE����AD��1������������y��![]() ��k��0����ͼ��ǡ�þ�����B�䣬D����k��ֵΪ_____��
��k��0����ͼ��ǡ�þ�����B�䣬D����k��ֵΪ_____��
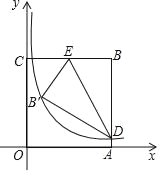
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬AB��5������B��BD��AB����C��D����AB�Ϸ���AD����BCD�����Բ��O�ڵ�E��
��1����֤����CAB����AEC��
��2����BC��3��
��EC��BD����AE�ij���
������BDCΪֱ�������Σ�����������������BD�ij���
��3����BC��EC��![]()
![]() ����
����![]() ���� ������ֱ��д��������ɣ�
���� ������ֱ��д��������ɣ�
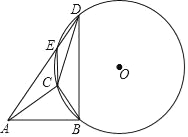
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB��3��AD��4��P������BD�˶�������AP�����߶�AP�Ƶ�P˳ʱ����ת90�����߶�PQ��
(1)����Q�䵽AD��ʱ����PAB��____����PA��_____��![]() ��Ϊ_____��
��Ϊ_____��
(2)��AP��BDʱ���Ǵ�ʱ��PΪP0����QΪQ0���ƶ���P��λ�ã����QQ0D�Ĵ�С��
(3)�ڵ�P�˶��У����Ե�QΪԲ�ģ�![]() BPΪ�뾶��Բ��ֱ��BD����ʱ����BP�ij��ȣ�
BPΪ�뾶��Բ��ֱ��BD����ʱ����BP�ij��ȣ�
(4)��P���߶�BD�ϣ���B��D�˶�����(����B��D����)�У���CQ��ȡֵ��Χ��ֱ��д�������
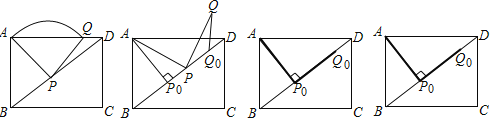
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
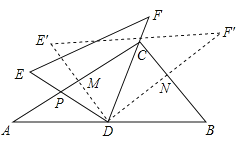
����Ŀ����һ�����dzߣ���Rt��ABC�У���ACB=90������B=60������Rt��EDF�У���EDF=90������E=45������ͼ�ڷţ���DΪAB���е㣬DE��AC�ڵ�P��DF������C.��Rt��EDF�Ƶ�D˳ʱ�뷽����ת������0��<��<60�㣩�� DE��AC�ڵ�M��DF��BC�ڵ�N����![]() ��ֵΪ( )
��ֵΪ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��![]() ��x�ύ�ڵ�A����y�ύ�ڵ�C��������
��x�ύ�ڵ�A����y�ύ�ڵ�C��������![]() ����A��C���㣬��x�����һ����Ϊ��B��
����A��C���㣬��x�����һ����Ϊ��B��
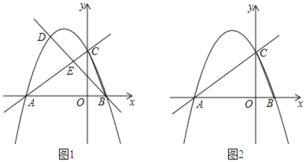
��1���������ߵĺ�������ʽ����2����DΪֱ��AC�Ϸ���������һ���㣬
������BC��CD��BD����BD��ֱ��AC�ڵ�E����CDE�����ΪS1����BCE�����ΪS2����![]() �����ֵ��
�����ֵ��
����ͼ2���Ƿ���ڵ�D��ʹ�á�DCA��2��BAC�������ڣ�ֱ��д����D�����꣬�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB��6��AD��4![]() ����E��BC���е㣬��F��AB�ϣ�FB��2��P�Ǿ�����һ���㣮����P�ӵ�F��������F��A��D��C��·���˶�������FPE��30��ʱ��FP�ij�Ϊ_____��
����E��BC���е㣬��F��AB�ϣ�FB��2��P�Ǿ�����һ���㣮����P�ӵ�F��������F��A��D��C��·���˶�������FPE��30��ʱ��FP�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com