
【题目】如图1,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C,抛物线
与x轴交于点A,与y轴交于点C,抛物线![]() 经过A、C两点,与x轴的另一交点为点B.
经过A、C两点,与x轴的另一交点为点B.
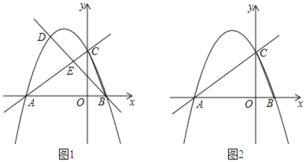
(1)求抛物线的函数表达式;(2)点D为直线AC上方抛物线上一动点,
①连接BC、CD、BD,设BD交直线AC于点E,△CDE的面积为S1,△BCE的面积为S2.求:![]() 的最大值;
的最大值;
②如图2,是否存在点D,使得∠DCA=2∠BAC?若存在,直接写出点D的坐标,若不存在,说明理由.
【答案】(1)![]() ;(2)①当
;(2)①当![]() 时,
时,![]() 的最大值是
的最大值是![]() ;②点D的坐标是
;②点D的坐标是![]()
【解析】
(1)根据题意得到A(-4,0),C(0,2)代入y=-![]() x2+bx+c,于是得到结论;
x2+bx+c,于是得到结论;
(2)①如图,令y=0,解方程得到x1=-4,x2=1,求得B(1,0),过D作DM⊥x轴于M,过B作BN⊥x轴交于AC于N,根据相似三角形的性质即可得到结论;
②根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形,取AB的中点P,求得P(-![]() ,0),得到PA=PC=PB=
,0),得到PA=PC=PB=![]() ,过D作x轴的平行线交y轴于R,交AC的延线于G,∠DCF=2∠BAC=∠DGC+∠CDG,解直角三角形即可得到结论.
,过D作x轴的平行线交y轴于R,交AC的延线于G,∠DCF=2∠BAC=∠DGC+∠CDG,解直角三角形即可得到结论.
解:(1)根据题意得A(-4,0),C(0,2),
∵抛物线y=-![]() x2+bx+c经过A.C两点,
x2+bx+c经过A.C两点,
∴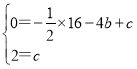 ,
,
∴![]() ,
,
抛物线解析式为:![]() ;
;
(2)①令![]() ,
,
∴![]()
解得:![]() ,
,![]()
∴B(1,0)
过点D作![]() 轴交AC于M,过点B作
轴交AC于M,过点B作![]() 轴交AC于点N,
轴交AC于点N,
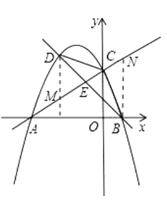
∴![]() ∥
∥![]()
∴![]()
∴![]()
设:![]()
∴![]()
∵![]()
∴![]()
∴
∴当![]() 时,
时,![]() 的最大值是
的最大值是![]() ;
;
②∵A(-4,0),B(1,0),C(0,2),
∴AC=2![]() ,BC=
,BC=![]() ,AB=5,
,AB=5,
∴AC2+BC2=AB2,
∴△ABC是以∠ACB为直角的直角三角形,
取AB的中点P,
∴P(-![]() ,0),
,0),
∴PA=PC=PB=![]() ,
,
∴∠CPO=2∠BAC,
∴tan∠CPO=tan(2∠BAC)=![]() ,
,
过D作x轴的平行线交y轴于R,交AC的延长线于G,如图,
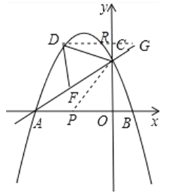
∴∠DCF=2∠BAC=∠DGC+∠CDG,
∴∠CDG=∠BAC,
∴tan∠CDG=tan∠BAC=![]() ,
,
即RC:DR=![]() ,
,
令D(a,-![]() a2-
a2-![]() a+2),
a+2),
∴DR=-a,RC=-![]() a2-
a2-![]() a,
a,
∴(-![]() a2-
a2-![]() a):(-a)=1:2,
a):(-a)=1:2,
∴a1=0(舍去),a2=-2,
∴xD=-2,
∴-![]() a2-
a2-![]() a+2=3,
a+2=3,
∴点D的坐标是![]()


科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了_____名学生,最喜欢用电话沟通的所对应扇形的圆心角是____°;
(2)将条形统计图补充完整;
(3)运用这次的调查结果估计1200名学生中最喜欢用QQ进行沟通的学生有多少名?
(4)甲、乙两名同学从微信,QQ,电话三种沟通方式中随机选了一种方式与对方联系,请用列表或画树状图的方法求出甲乙两名同学恰好选中同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为有效利用电力资源,某市电力局采用“峰谷”用电政策,每天8:00﹣22:00为“峰时段”,22:00至次日8:00为“谷时段”.嘉淇家使用的是峰谷电价,他将家里2018年1月至5月的峰时段和谷时段用电量绘制成如图所示的条形统计图,已知嘉淇家1月份电费为51.8元,2月份电费为50.85元.
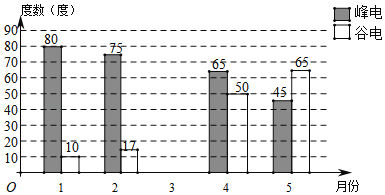
(1)“峰电”每度 元,“谷电”每度 ;
(2)嘉淇家3月份用电量比这5个月的平均用电量少1度,且3月份所交电费为49.54元,则3月份“峰电”度数为 度;
(3)2018年6月,嘉淇单位决定给职工补贴前五个月中的两个月份的电费,求恰好选中3月份和4月份的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立一个可自由转动的转盘,(如图,3个数字所在的扇形面积相等)并规定,顾客每购满100元商品,可转动两次转盘,转盘停止后,看指针指向的数.(如果指针指向分界线,则重新转动转盘,直到指针指向数为止)获奖方法是:①指针两次都指向3,顾客可获得90元购物券,②指针只有一次指向3,顾客可得36元购物券,③指针两次都不指向3,顾客只能获得18元购物券;若顾客不愿转动转盘,则可直接获得30元购物券
(1)试用树状图或列表法给出两次转动转盘指针所有可能指向的结果;
(2)请分别求顾客获得90元,36元,18元购物券的概率;
(3)你认为转动转盘和直接获得购物券哪种方式更合算?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆;两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计,EF长度远大于车辆宽度),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,该地下车库出口的车辆限高标志牌设置如图4是否合理?请通过计算说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
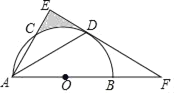
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=6![]() ,求阴影区域的面积.(结果保留根号和π)
,求阴影区域的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com