
ЁОЬтФПЁПЮЊгааЇРћгУЕчСІзЪдДЃЌФГЪаЕчСІОжВЩгУЁАЗхЙШЁБгУЕчеўВпЃЌУПЬь8ЃК00Љ22ЃК00ЮЊЁАЗхЪБЖЮЁБЃЌ22ЃК00жСДЮШе8ЃК00ЮЊЁАЙШЪБЖЮЁБЃЎМЮфПМвЪЙгУЕФЪЧЗхЙШЕчМлЃЌЫћНЋМвРя2018Фъ1дТжС5дТЕФЗхЪБЖЮКЭЙШЪБЖЮгУЕчСПЛцжЦГЩШчЭМЫљЪОЕФЬѕаЮЭГМЦЭМЃЌвбжЊМЮфПМв1дТЗнЕчЗбЮЊ51.8дЊЃЌ2дТЗнЕчЗбЮЊ50.85дЊЃЎ
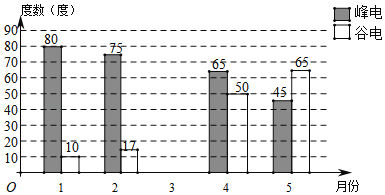
ЃЈ1ЃЉЁАЗхЕчЁБУПЖШЁЁ дЊЃЌЁАЙШЕчЁБУПЖШЁЁ ЃЛ
ЃЈ2ЃЉМЮфПМв3дТЗнгУЕчСПБШет5ИідТЕФЦНОљгУЕчСПЩй1ЖШЃЌЧв3дТЗнЫљНЛЕчЗбЮЊ49.54дЊЃЌдђ3дТЗнЁАЗхЕчЁБЖШЪ§ЮЊЁЁ ЖШЃЛ
ЃЈ3ЃЉ2018Фъ6дТЃЌМЮфПЕЅЮЛОіЖЈИјжАЙЄВЙЬљЧАЮхИідТжаЕФСНИідТЗнЕФЕчЗбЃЌЧѓЧЁКУбЁжа3дТЗнКЭ4дТЗнЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ0.61ЃЌ0.3ЃЛЃЈ2ЃЉ64ЃЛЃЈ3ЃЉPЃЈбЁжа3дТЗнКЭ4дТЗнЃЉЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшЁАЗхЕчЁБУПЖШxдЊЃЌЁАЙШЕчЁБУПЖШyдЊЃЌгЩЬѕаЮЭГМЦБэЕУГіЗНГЬзщЃЌНтЗНГЬзщМДПЩЃЛ
ЃЈ2ЃЉЩшМЮфПМв3дТЗнЁАЗхЕчЁБЖШЪ§ЮЊxЃЌЁАЙШЕчЁБЖШЪ§ЮЊyЃЌИљОнЬтвтЕУГіЗНГЬзщЃЌНтЗНГЬзщМДПЩЃЛ
ЃЈ3ЃЉгЩСаБэЗЈЕУГіЙВга20жжЕШПЩФмЪТМўЃЌгЩИХТЪЙЋЪНМДПЩЕУГіНсЙћЃЎ
ЃЈ1ЃЉЩшЁАЗхЕчЁБУПЖШxдЊЃЌЁАЙШЕчЁБУПЖШyдЊЃЌ
гЩЬѕаЮЭГМЦБэЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрЁАЗхЕчЁБУПЖШ0.61дЊЃЌЁАЙШЕчЁБУПЖШ0.3дЊЃЌ
ЙЪД№АИЮЊ0.61ЃЌ0.3ЃЛ
ЃЈ2ЃЉЩшМЮфПМв3дТЗнЁАЗхЕчЁБЖШЪ§ЮЊxЃЌЁАЙШЕчЁБЖШЪ§ЮЊyЃЌ
ИљОнЬтвтЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрМЮфПМв3дТЗнЁАЗхЕчЁБЖШЪ§ЮЊ64ЃЌ
ЙЪД№АИЮЊЃК64ЃЛ
ЃЈ3ЃЉЧАЮхИідТжаЕФбЁжаШЮСНИідТЗнЧщПіСаБэШчЯТЃК
1 | 2 | 3 | 4 | 5 | |
1 | ЃЈ1ЃЌ2ЃЉ | ЃЈ1ЃЌ3ЃЉ | ЃЈ1ЃЌ4ЃЉ | ЃЈ1ЃЌ5ЃЉ | |
2 | ЃЈ2ЃЌ1ЃЉ | ЃЈ2ЃЌ3ЃЉ | ЃЈ2ЃЌ4ЃЉ | ЃЈ2ЃЌ5ЃЉ | |
3 | ЃЈ3ЃЌ1ЃЉ | ЃЈ3ЃЌ2ЃЉ | 3ЃЌ4ЃЉ | ЃЈ3ЃЌ5ЃЉ | |
4 | ЃЈ4ЃЌ1ЃЉ | ЃЈ4ЃЌ2ЃЉ | ЃЈ4ЃЌ3ЃЉ | ЃЈ4ЃЌ5ЃЉ | |
5 | ЃЈ5ЃЌ1ЃЉ | ЃЈ5ЃЌ2ЃЉ | ЃЈ5ЃЌ3ЃЉ | ЃЈ5ЃЌ4ЃЉ |
ЙВга20жжЕШПЩФмЪТМўЃЌбЁжа3дТЗнКЭ4дТЗнЕФНсЙћга2ИіЃЌ
ЁрPЃЈбЁжа3дТЗнКЭ4дТЗнЃЉЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕк36НьШЋЙњаХЯЂбЇЖЌСюгЊдкЙужнТфЯТсЁФЛЃЌГЄПЄЪІЩњЩСвЋИїДѓШќГЁЃЌН№ХЦЪ§ЁЂНБХЦЪ§ОљЮШОгКўФЯЪЁЕквЛЃЎбЇаЃФтдЄЫу7700дЊШЋВПгУгкЙКТђМзЁЂввЁЂБћШ§жжЭМЪщЙВ20ЬзНБРјЛёНБЪІЩњЃЌЦфжаМзжжЭМЪщУПЬз500дЊЃЌввжжЭМЪщУПЬз400дЊЃЌБћжжЭМЪщУПЬз250дЊЃЌЩшЙКТђМзжжЭМЪщxЬзЃЌввжжЭМЪщyЬзЃЌЧыНтД№ЯТСаЮЪЬтЃК
(1)ЧыЧѓГіyгыxЕФКЏЪ§ЙиЯЕЪН(ВЛашвЊаДГіздБфСПЕФШЁжЕЗЖЮЇ)ЃЛ
(2)ШєбЇаЃЙКТђЕФМзЁЂввСНжжЭМЪщЙВ14ЬзЃЌЧѓМзЁЂввЭМЪщИїЖрЩйЬзЃП
(3)ШєбЇаЃЙКТђЕФМзЁЂввСНжжЭМЪщОљВЛЩйгк1ЬзЃЌдђгаФФМИжжЙКТђЗНАИЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
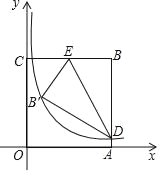
ЁОЬтФПЁПШчЭМЃЌОиаЮOABCЕФБпOAЃЌOCЗжБ№дкxжсЃЌyжсЩЯЃЌOCЃН7ЃЌЕуBдкЕквЛЯѓЯоЃЌЕуDдкБпABЩЯЃЌЕуEдкБпBCЩЯЃЌЧвЁЯBDEЃН30ЁуЃЌНЋЁїBDEбиDEелЕўЕУЕНЁїBЁфDEЃЎШєADЃН1ЃЌЗДБШР§КЏЪ§yЃН![]() ЃЈkЁй0ЃЉЕФЭМЯѓЧЁКУОЙ§ЕуBЁфЃЌDЃЌдђkЕФжЕЮЊ_____ЃЎ
ЃЈkЁй0ЃЉЕФЭМЯѓЧЁКУОЙ§ЕуBЁфЃЌDЃЌдђkЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
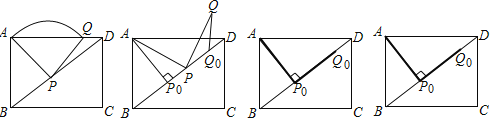
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН3ЃЌADЃН4ЃЌPбиЩфЯпBDдЫЖЏЃЌСЌНгAPЃЌНЋЯпЖЮAPШЦЕуPЫГЪБеыа§зЊ90ЁуЕУЯпЖЮPQЃЎ
(1)ЕБЕуQТфЕНADЩЯЪБЃЌЁЯPABЃН____ЁуЃЌPAЃН_____ЃЌ![]() ГЄЮЊ_____ЃЛ
ГЄЮЊ_____ЃЛ
(2)ЕБAPЁЭBDЪБЃЌМЧДЫЪБЕуPЮЊP0ЃЌЕуQЮЊQ0ЃЌвЦЖЏЕуPЕФЮЛжУЃЌЧѓЁЯQQ0DЕФДѓаЁЃЛ
(3)дкЕуPдЫЖЏжаЃЌЕБвдЕуQЮЊдВаФЃЌ![]() BPЮЊАыОЖЕФдВгыжБЯпBDЯрЧаЪБЃЌЧѓBPЕФГЄЖШЃЛ
BPЮЊАыОЖЕФдВгыжБЯпBDЯрЧаЪБЃЌЧѓBPЕФГЄЖШЃЛ
(4)ЕуPдкЯпЖЮBDЩЯЃЌгЩBЯђDдЫЖЏЙ§ГЬ(АќКЌBЁЂDСНЕу)жаЃЌЧѓCQЕФШЁжЕЗЖЮЇЃЌжБНгаДГіНсЙћЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
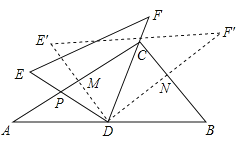
ЁОЬтФПЁПНЋвЛИБШ§НЧГпЃЈдкRtІЄABCжаЃЌЁЯACB=90ЁуЃЌЁЯB=60ЁуЃЛдкRtІЄEDFжаЃЌЁЯEDF=90ЁуЃЌЁЯE=45ЁуЃЉШчЭМАкЗХЃЌЕуDЮЊABЕФжаЕуЃЌDEНЛACгкЕуPЃЌDFОЙ§ЕуC.НЋRtІЄEDFШЦЕуDЫГЪБеыЗНЯђа§зЊНЧІСЃЈ0Ёу<ІС<60ЁуЃЉЃЌ DEНЛACгкЕуMЃЌDFНЛBCгкЕуNЃЌдђ![]() ЕФжЕЮЊ( )
ЕФжЕЮЊ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
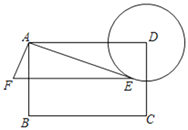
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌABЃН6ЃЌBCЃН9ЃЌвдDЮЊдВаФЃЌ3ЮЊАыОЖзїЁбDЃЌEЮЊЁбDЩЯвЛЖЏЕуЃЌСЌНгAEЃЌвдAEЮЊжБНЧБпзїRtЁїAEFЃЌЪЙЁЯEAFЃН90ЁуЃЌtanЁЯAEFЃН![]() ЃЌдђЕуFгыЕуCЕФзюаЁОрРыЮЊ_____ЃЎ
ЃЌдђЕуFгыЕуCЕФзюаЁОрРыЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуCЃЌХзЮяЯп
гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуCЃЌХзЮяЯп![]() ОЙ§AЁЂCСНЕуЃЌгыxжсЕФСэвЛНЛЕуЮЊЕуBЃЎ
ОЙ§AЁЂCСНЕуЃЌгыxжсЕФСэвЛНЛЕуЮЊЕуBЃЎ
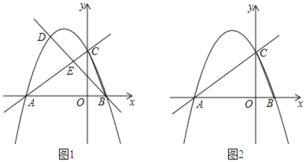
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛЃЈ2ЃЉЕуDЮЊжБЯпACЩЯЗНХзЮяЯпЩЯвЛЖЏЕуЃЌ
ЂйСЌНгBCЁЂCDЁЂBDЃЌЩшBDНЛжБЯпACгкЕуEЃЌЁїCDEЕФУцЛ§ЮЊS1ЃЌЁїBCEЕФУцЛ§ЮЊS2ЃЎЧѓЃК![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЂкШчЭМ2ЃЌЪЧЗёДцдкЕуDЃЌЪЙЕУЁЯDCAЃН2ЁЯBACЃПШєДцдкЃЌжБНгаДГіЕуDЕФзјБъЃЌШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
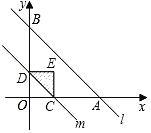
ЁОЬтФПЁПШчЭМЃЌжБЯпlЕФНтЮіЪНЮЊyЃНЉx+4ЃЌЫќгыxжсКЭyжсЗжБ№ЯрНЛгкAЃЌBСНЕуЃЎЦНаагкжБЯпlЕФжБЯпmДгдЕуOГіЗЂЃЌбиxжсЕФе§ЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЎЫќгыxжсКЭyжсЗжБ№ЯрНЛгкCЃЌDСНЕуЃЌдЫЖЏЪБМфЮЊtУыЃЈ0ЁмtЁм4ЃЉЃЌвдCDЮЊаББпзїЕШбќжБНЧШ§НЧаЮCDEЃЈEЃЌOСНЕуЗжБ№дкCDСНВрЃЉЃЎШєЁїCDEКЭЁїOABЕФжиКЯВПЗжЕФУцЛ§ЮЊSЃЌдђSгыtжЎМфЕФКЏЪ§ЙиЯЕЕФЭМЯѓДѓжТЪЧЃЈЁЁЁЁЃЉ
A. 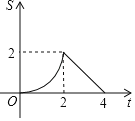 B.
B. 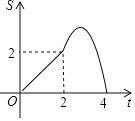
C. 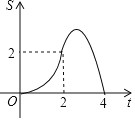 D.
D. 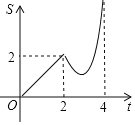
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉМЦЫуЃК ![]() Љ2sin45Ёу+ЃЈ2ЉІаЃЉ0ЉЃЈ
Љ2sin45Ёу+ЃЈ2ЉІаЃЉ0ЉЃЈ![]() ЃЉЉ1ЃЛ
ЃЉЉ1ЃЛ
ЃЈ2ЃЉЯШЛЏМђЃЌдйЧѓжЕ![]() ЃЈa2Љb2ЃЉЃЌЦфжаa=
ЃЈa2Љb2ЃЉЃЌЦфжаa=![]() ЃЌb=Љ2
ЃЌb=Љ2![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com