
ĄŸÌâÄżĄżÈçÍŒŁŹÖ±Ïßl”ÄœâÎöÊœÎȘyŁœ©x+4ŁŹËüÓëxÖáșÍyÖá·Ö±đÏàœ»ÓÚAŁŹBÁœ”ăŁźÆœĐĐÓÚÖ±Ïßl”ÄÖ±ÏßmŽÓÔ”ăOłö·ąŁŹŃŰxÖá”ÄŐę·œÏòÒÔĂżĂë1žö”„λł€¶È”ÄËÙ¶ÈÔ˶ŻŁźËüÓëxÖáșÍyÖá·Ö±đÏàœ»ÓÚCŁŹDÁœ”㣏Ô˶ŻÊ±ŒäÎȘtĂ룚0ĄÜtĄÜ4Ł©ŁŹÒÔCDÎȘб±ßŚś”ÈŃüÖ±œÇÈęœÇĐÎCDEŁšEŁŹOÁœ”ă·Ö±đÔÚCDÁœČàŁ©ŁźÈôĄśCDEșÍĄśOAB”ÄÖŰșÏČż·Ö”ÄĂæ»ęÎȘSŁŹÔòSÓëtÖźŒä”ÄșŻÊęčŰÏ””ÄÍŒÏóŽóÖÂÊÇŁšĄĄĄĄŁ©
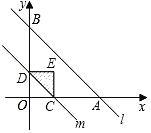
A. 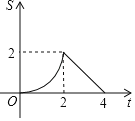 B.
B. 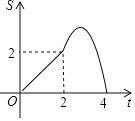
C. 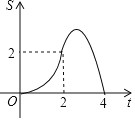 D.
D. 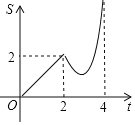
 ÖÇÈ€ÊîŒÙÎÂčÊÖȘĐÂÏ”ÁĐŽđ°ž
ÖÇÈ€ÊîŒÙÎÂčÊÖȘĐÂÏ”ÁĐŽđ°ž ÓąÓïĐĄÓąĐÛÌìÌìÄŹĐŽÏ”ÁĐŽđ°ž
ÓąÓïĐĄÓąĐÛÌìÌìÄŹĐŽÏ”ÁĐŽđ°ž ÊîŒÙŚśÒ”°Č»ŐÉÙÄê¶ùÍŻłö°æÉçÏ”ÁĐŽđ°ž
ÊîŒÙŚśÒ”°Č»ŐÉÙÄê¶ùÍŻłö°æÉçÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘ”ăA(©3ŁŹy1)ŁŹB(2ŁŹy2)ŸùÔÚĆŚÎïÏßyŁœax2+bx+cÉÏŁŹ”ăP(mŁŹn)ÊÇžĂĆŚÎïÏߔĶ„”㣏Èôy1ŁŸy2ĄĘnŁŹÔòm”ÄÈĄÖ”·¶Î§ÊÇ(ĄĄĄĄ)
A.©3ŁŒmŁŒ2B.©![]() ŁŒmŁŒ-
ŁŒmŁŒ-![]() C.mŁŸ©
C.mŁŸ©![]() D.mŁŸ2
D.mŁŸ2
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎȘÓĐЧÀûÓĂ”çÁŠŚÊÔŽŁŹÄłÊĐ”çÁŠŸÖČÉÓĂĄ°·ćčÈĄ±ÓĂ”çŐțČߣŹĂżÌì8Łș00©22Łș00ÎȘĄ°·ćʱ¶ÎĄ±ŁŹ22Łș00ÖÁŽÎÈŐ8Łș00ÎȘĄ°čÈʱ¶ÎĄ±ŁźŒÎäżŒÒÊčÓĂ”ÄÊÇ·ćčÈ”çŒÛŁŹËûœ«ŒÒÀï2018Äê1ÔÂÖÁ5Ô”ķćʱ¶ÎșÍčÈʱ¶ÎÓĂ”çÁż»æÖÆłÉÈçÍŒËùÊŸ”ÄÌőĐÎÍłŒÆÍŒŁŹÒŃÖȘŒÎäżŒÒ1Ô·ʔç·ŃÎȘ51.8ÔȘŁŹ2Ô·ʔç·ŃÎȘ50.85ÔȘŁź
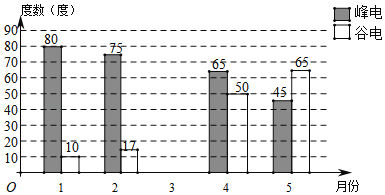
Łš1Ł©Ą°·ć”祱ÿ¶ÈĄĄ ÔȘŁŹĄ°čÈ”çĄ±Ăż¶ÈĄĄ Ł»
Łš2Ł©ŒÎäżŒÒ3Ô·ĘÓĂ”çÁż±ÈŐâ5žöÔ”ÄÆœŸùÓĂ”çÁżÉÙ1¶ÈŁŹÇÒ3Ô·ĘËùœ»”ç·ŃÎȘ49.54ÔȘŁŹÔò3Ô·ʥ°·ć”祱¶ÈÊęÎȘĄĄ ¶ÈŁ»
Łš3Ł©2018Äê6ÔÂŁŹŒÎäż”„λŸö¶šžűÖ°č€ČčÌùÇ°ÎćžöÔÂÖĐ”ÄÁœžöÔ·ʔĔç·ŃŁŹÇóÇĄșĂŃĄÖĐ3Ô·ĘșÍ4Ô·ʔĞĆÂÊŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄł”ŰÏÂł”żâłöżÚŽŠ°ČŚ°ÁËĄ°Áœ¶ÎÊœÀžžËĄ±ŁŹÈçÍŒ1ËùÊŸŁŹ”ăAÊÇÀžžËŚȘ¶Ż”ÄÖ§”㣏”ăEÊÇÀžžËŁ»Áœ¶Î”ÄÁȘœá”㣟”±ł”ÁŸŸčęʱŁŹÀžžËAEFŚî¶àÖ»ÄÜÉęÆđ”œÈçÍŒ2ËùÊŸ”ÄλÖĂŁŹÆäÊŸÒâÍŒÈçÍŒ3ËùÊŸŁšÀžžËżí¶ÈșöÂÔČ»ŒÆŁŹEFł€¶ÈÔ¶ŽóÓÚł”ÁŸżí¶ÈŁ©ŁŹÆäÖĐABĄÍBCŁŹEFĄÎBCŁŹĄÏAEFŁœ143ĄăŁŹABŁœAEŁœ1.2ĂŚŁŹžĂ”ŰÏÂł”żâłöżÚ”Äł”ÁŸÏȚžß±êÖŸĆÆÉèÖĂÈçÍŒ4ÊÇ·ńșÏÀíŁżÇëÍščęŒÆËă˔ÜÀíÓÉŁźŁšČÎżŒÊęŸĘŁșsin37ĄăĄÖ0.60ŁŹcos37ĄăĄÖ0.80ŁŹtan37ĄăĄÖ0.75Ł©

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
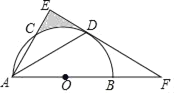
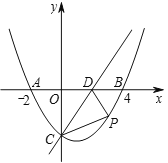
ĄŸÌâÄżĄżÈçÍŒŁŹABÎȘ°ëÔČO”ÄÖ±Ÿ¶ŁŹACÊÇĄŃO”ÄÒ»ÌőÏÒŁŹDÎȘ![]() ”ÄÖД㣏ŚśDEĄÍACŁŹœ»AB”ÄŃÓł€ÏßÓÚ”ăFŁŹÁŹœÓDAŁź
”ÄÖД㣏ŚśDEĄÍACŁŹœ»AB”ÄŃÓł€ÏßÓÚ”ăFŁŹÁŹœÓDAŁź
Łš1Ł©ÇóÖ€ŁșEFÎȘ°ëÔČO”ÄÇĐÏߣ»
Łš2Ł©ÈôDAŁœDFŁœ6![]() ŁŹÇóÒőÓ°ÇűÓò”ÄĂæ»ęŁźŁšœáčû±ŁÁôžùșĆșÍŠĐŁ©
ŁŹÇóÒőÓ°ÇűÓò”ÄĂæ»ęŁźŁšœáčû±ŁÁôžùșĆșÍŠĐŁ©
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŁš6·ÖŁ©ÄłșŁÓòÓĐAŁŹBÁœžöžÛżÚŁŹBžÛżÚÔÚAžÛżÚ±±Æ«Îś30Ąă·œÏòÉÏŁŹŸàAžÛżÚ60șŁÀïŁŹÓĐÒ»ËÒŽŹŽÓAžÛżÚłö·ąŁŹŃ۶«±±·œÏòĐĐʻһ¶ÎŸàÀëșóŁŹ”œŽïλÓÚBžÛżÚÄÏÆ«¶«75Ąă·œÏò”ÄCŽŠŁŹÇóžĂŽŹÓëBžÛżÚÖźŒä”ÄŸàÀ댎CB”Äł€Łšœáčû±ŁÁôžùșĆŁ©Łź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÓĂłßčæÔÚÒ»žöÆœĐĐËıßĐÎÄÚŚśÁâĐÎABCDŁŹÏÂÁĐŚś·šÖĐŽíÎó”ÄÊÇ(ĄĄĄĄ)
A. 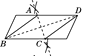 B.
B. 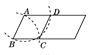 C.
C. 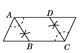 D.
D. 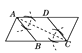
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
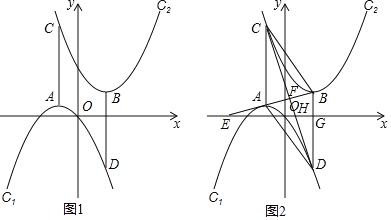
ĄŸÌâÄżĄżÒŃÖȘŁșĆŚÎïÏßC1ŁșyŁœ©Łšx+mŁ©2+m2ŁšmŁŸ0Ł©ŁŹĆŚÎïÏßC2ŁșyŁœŁšx©nŁ©2+n2ŁšnŁŸ0Ł©ŁŹłÆĆŚÎïÏßC1ŁŹC2»„ÎȘĆɶÔĆŚÎïÏߣŹÀęÈçĆŚÎïÏßC1ŁșyŁœ©Łšx+1Ł©2+1ÓëĆŚÎïÏßC2ŁșyŁœŁšx©![]() Ł©2+2ÊÇĆɶÔĆŚÎïÏߣŹÒŃÖȘĆɶÔĆŚÎïÏßC1ŁŹC2”Ķ„”ă·Ö±đÎȘAŁŹBŁŹĆŚÎïÏßC1”ĶԳÆÖáœ»ĆŚÎïÏßC2ÓÚCŁŹĆŚÎïÏßC2”ĶԳÆÖáœ»ĆŚÎïÏßC1ÓëDŁź
Ł©2+2ÊÇĆɶÔĆŚÎïÏߣŹÒŃÖȘĆɶÔĆŚÎïÏßC1ŁŹC2”Ķ„”ă·Ö±đÎȘAŁŹBŁŹĆŚÎïÏßC1”ĶԳÆÖáœ»ĆŚÎïÏßC2ÓÚCŁŹĆŚÎïÏßC2”ĶԳÆÖáœ»ĆŚÎïÏßC1ÓëDŁź
Łš1Ł©ÒŃÖȘĆŚÎïÏßąÙyŁœ©x2©2xŁŹąÚyŁœŁšx©3Ł©2+3ŁŹąÛyŁœŁšx©![]() Ł©2+2ŁŹąÜyŁœx2©x+
Ł©2+2ŁŹąÜyŁœx2©x+![]() ŁŹÔòĆŚÎïÏßąÙąÚąÛąÜÖĐ»„ÎȘĆɶÔĆŚÎïÏß”ÄÊÇĄĄ ĄĄŁšÇëÔÚșáÏßÉÏÌîĐŽĆŚÎïÏß”ÄÊęŚÖĐòșĆŁ©Ł»
ŁŹÔòĆŚÎïÏßąÙąÚąÛąÜÖĐ»„ÎȘĆɶÔĆŚÎïÏß”ÄÊÇĄĄ ĄĄŁšÇëÔÚșáÏßÉÏÌîĐŽĆŚÎïÏß”ÄÊęŚÖĐòșĆŁ©Ł»
Łš2Ł©ÈçÍŒ1ŁŹ”±mŁœ1ŁŹnŁœ2ʱŁŹÖ€ĂśACŁœBDŁ»
Łš3Ł©ÈçÍŒ2ŁŹÁŹœÓABŁŹCDœ»ÓÚ”ăFŁŹŃÓł€BAœ»xÖá”Äžș°ëÖáÓÚ”ăEŁŹŒÇBDœ»xÖáÓÚGŁŹCDœ»xÖáÓÚ”ăHŁŹĄÏBEOŁœĄÏBDCŁź
ąÙÇóÖ€ŁșËıßĐÎACBDÊÇÁâĐÎŁ»
ąÚÈôÒŃÖȘĆŚÎïÏßC2ŁșyŁœŁšx©2Ł©2+4ŁŹÇëÇółöm”ÄÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹĆŚÎïÏß![]() Óë
Óë![]() Ö᜻ÓÚ”ă
Ö᜻ÓÚ”ă![]() ŁŹ
ŁŹ![]() ŁŹÓëÖ±Ïß
ŁŹÓëÖ±Ïß![]() œ»ÓÚ”ă
œ»ÓÚ”ă![]() ŁŹÖ±Ïß
ŁŹÖ±Ïß![]() Óë
Óë![]() Ö᜻ÓÚ”ă
Ö᜻ÓÚ”ă![]() Łź
Łź
(1)ÇóžĂĆŚÎïÏߔĜâÎöÊœŁź
(2)”ă![]() ÊÇĆŚÎïÏßÉÏ”ÚËÄÏóÏȚÉÏ”ÄÒ»žö¶Ż”㣏ÁŹœÓ
ÊÇĆŚÎïÏßÉÏ”ÚËÄÏóÏȚÉÏ”ÄÒ»žö¶Ż”㣏ÁŹœÓ![]() ŁŹ
ŁŹ![]() ŁŹ”±
ŁŹ”±![]() ”ÄĂæ»ęŚîŽóʱŁŹÇó”ă
”ÄĂæ»ęŚîŽóʱŁŹÇó”ă![]() ”ÄŚű±êŁź
”ÄŚű±êŁź
(3)œ«ĆŚÎïÏߔĶԳÆÖáÏòŚóÆœÒÆ3žöł€¶È”„λ”Ă”œÖ±Ïß![]() ŁŹ”ă
ŁŹ”ă![]() ÊÇÖ±Ïß
ÊÇÖ±Ïß![]() ÉÏÒ»”㣏ÁŹœÓ
ÉÏÒ»”㣏ÁŹœÓ![]() ŁŹ
ŁŹ![]() ŁŹÈôÖ±Ïß
ŁŹÈôÖ±Ïß![]() ÉÏŽæÔÚÊč
ÉÏŽæÔÚÊč![]() ŚîŽó”Ä”ă
ŚîŽó”Ä”ă![]() ŁŹÇëÖ±œÓĐŽłöÂúŚăÌőŒț”Ä”ă
ŁŹÇëÖ±œÓĐŽłöÂúŚăÌőŒț”Ä”ă![]() ”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź
”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com