
【题目】如图,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,使∠EAF=90°,tan∠AEF=![]() ,则点F与点C的最小距离为_____.
,则点F与点C的最小距离为_____.
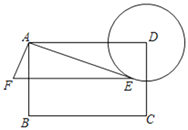
【答案】3![]() ﹣1 .
﹣1 .
【解析】
如图,取AB的中点G,连接FG,根据已知条件易证△AFG∽△EAD,根据相似三角形的性质求得FG=1;即可得点F在以点G为圆心,半径为1的圆上,所以当点F在线段GC上时,点F与点C的距离最小,由此即可求得点F与点C的最小距离.
如图,取AB的中点G,连接FG,
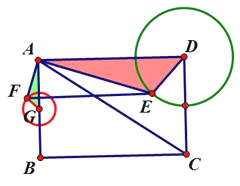
∵AB=4,AD=6,
∴AG=2,![]() ;
;
在Rt△AEF,∠EAF=90°,tan∠AEF=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠EAF=∠BAD=90°,
∴∠FAG=∠EAD,
∴△AFG∽△EAD,
∴![]() ,
,
∵DE=3,
∴FG=1;
∵点E为⊙D上一动点,
∴点F在以点G为圆心,半径为1的圆上,
∴当点F在线段GC上时,点F与点C的距离最小,
在Rt△GBC中,BC=6,GB=3,由勾股定理求得GC=3![]() ,
,
∴FC=3![]() ﹣1.
﹣1.
即点F与点C的最小距离为3![]() ﹣1.
﹣1.
故答案为:3![]() ﹣1.
﹣1.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某校图书馆为了满足同学们阅读课外书的需求,计划购进甲、乙两种图书共100套,其中甲种图书每套120元,乙种图书每套80元.设购买甲种图书的数量![]() 套.
套.
(1)按计划用11000元购进甲、乙两种图书时,问购进这甲、乙两种图书各多少套?
(2)若购买甲种图书的数量要不少于乙种图书的数量的![]() ,购买两种图书的总费用为
,购买两种图书的总费用为![]() 元,求出最少总费用.
元,求出最少总费用.
(3)图书馆在不增加购买数量的情况下,增加购买丙种图书,要求甲种图书与丙种图书的购买费用相同.丙种图书每套100元,总费用比(2)中最少总费用多出1240元,请直接写出购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(1)已知∠APB是⊙O上关于点A、B的滑动角,
①若AB是⊙O的直径,则∠APB= °;
②若⊙O的半径是1,AB=![]() ,求∠APB的度数;
,求∠APB的度数;
(2)已知O2是⊙O1外一点,以O2为圆心作一个圆与⊙O1相交于A、B两点,∠APB是⊙O1上关于点A、B的滑动角,直线PA、PB分别交⊙O2于M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系.
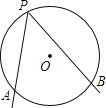
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为有效利用电力资源,某市电力局采用“峰谷”用电政策,每天8:00﹣22:00为“峰时段”,22:00至次日8:00为“谷时段”.嘉淇家使用的是峰谷电价,他将家里2018年1月至5月的峰时段和谷时段用电量绘制成如图所示的条形统计图,已知嘉淇家1月份电费为51.8元,2月份电费为50.85元.
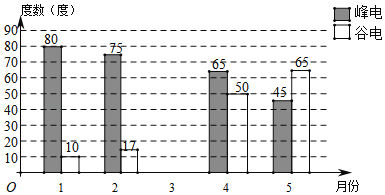
(1)“峰电”每度 元,“谷电”每度 ;
(2)嘉淇家3月份用电量比这5个月的平均用电量少1度,且3月份所交电费为49.54元,则3月份“峰电”度数为 度;
(3)2018年6月,嘉淇单位决定给职工补贴前五个月中的两个月份的电费,求恰好选中3月份和4月份的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知动点P以2cm/s的速度沿如图所示的边框从B-C-D-E-F-A的路径运动,记△ABP的面积为S (cm2), S与运动时间t (s)的关系如图所示,若AB=6cm,请回答下列问题:
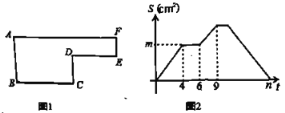
(1)如图中BC=______cm, CD=______cm,DE=______cm
(2)求出如图中边框所围成图形的面积;
(3)求如图中m、n的值;
(4)分别求出当点P在线段BC和DE上运动时S与t的关系式,并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆;两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计,EF长度远大于车辆宽度),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,该地下车库出口的车辆限高标志牌设置如图4是否合理?请通过计算说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与B港口之间的距离即CB的长(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com