
【题目】如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(1)已知∠APB是⊙O上关于点A、B的滑动角,
①若AB是⊙O的直径,则∠APB= °;
②若⊙O的半径是1,AB=![]() ,求∠APB的度数;
,求∠APB的度数;
(2)已知O2是⊙O1外一点,以O2为圆心作一个圆与⊙O1相交于A、B两点,∠APB是⊙O1上关于点A、B的滑动角,直线PA、PB分别交⊙O2于M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系.
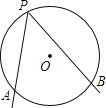
【答案】(1)①90°;②45°或90°;(2)详见解析.
【解析】
(1)①根据直径所对的圆周角等于90°即可求解;
②根据勾股定理的逆定理可得∠AOB=90°,再分点P在优弧![]() 上;点P在劣弧
上;点P在劣弧![]() 上两种情况讨论求解;
上两种情况讨论求解;
(2)根据点P在⊙O1上的位置分为四种情况得到∠APB与∠MAN、∠ANB之间的数量关系.
解:(1)①若AB是⊙O的直径,则∠APB=90.
②如图,连接AB、OA、OB.
在△AOB中,
∵OA=OB=1.AB=![]() ,
,
∴OA2+OB2=AB2.
∴∠AOB=90°.
当点P在优弧![]() 上时,∠APB=
上时,∠APB=![]() ∠AOB=45°;
∠AOB=45°;
当点P在劣弧![]() 上时,∠AP′B=
上时,∠AP′B=![]() (360°﹣∠AOB)=135°
(360°﹣∠AOB)=135°
(2)根据点P在⊙O1上的位置分为以下四种情况.
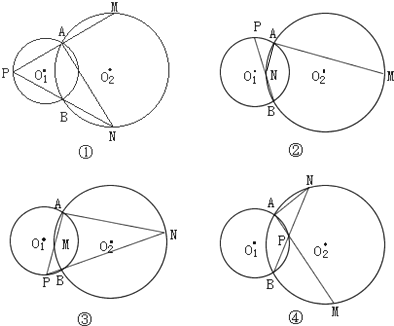
第一种情况:点P在⊙O2外,且点A在点P与点M之间,点B在点P与点N之间,如图①
∵∠MAN=∠APB+∠ANB,
∴∠APB=∠MAN﹣∠ANB;
第二种情况:点P在⊙O2外,且点A在点P与点M之间,点N在点P与点B之间,如图②.
∵∠MAN=∠APB+∠ANP=∠APB+(180°﹣∠ANB),
∴∠APB=∠MAN+∠ANB﹣180°;
第三种情况:点P在⊙O2外,且点M在点P与点A之间,点B在点P与点N之间,如图③.
∵∠APB+∠ANB+∠MAN=180°,
∴∠APB=180°﹣∠MAN﹣∠ANB,
第四种情况:点P在⊙O2内,如图④,
∠APB=∠MAN+∠ANB.
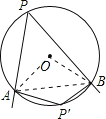


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
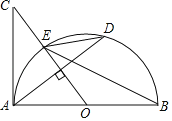
【题目】如图,AB是半圆O的直径,D为半圆上的一个动点(不与点A,B重合),连接AD,过点O作AD的垂线,交半圆O的切线AC于点C,交半圆O于点E.连接BE,DE.
(1)求证:∠BED=∠C.
(2)连接BD,OD,CD.
填空:
①当∠ACO的度数为 时,四边形OBDE为菱形;
②当∠ACO的度数为 时,四边形AODC为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
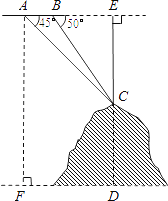
【题目】如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
查看答案和解析>>
科目:初中数学 来源: 题型:
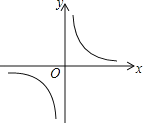
【题目】反比例函数y=![]() 的图象如图所示,以下结论:①常数m<﹣1;②在每个象限内,y随x的增大而增大;③若点A(﹣1,h),B(2,k)在图象上,则h<k;④若点P(x,y)在上,则点P′(﹣x,﹣y)也在图象.其中正确结论的个数是( )
的图象如图所示,以下结论:①常数m<﹣1;②在每个象限内,y随x的增大而增大;③若点A(﹣1,h),B(2,k)在图象上,则h<k;④若点P(x,y)在上,则点P′(﹣x,﹣y)也在图象.其中正确结论的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
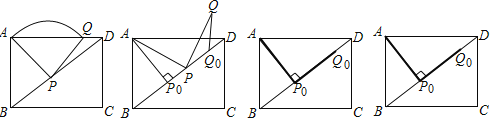
【题目】如图,在矩形ABCD中,AB=3,AD=4,P沿射线BD运动,连接AP,将线段AP绕点P顺时针旋转90°得线段PQ.
(1)当点Q落到AD上时,∠PAB=____°,PA=_____,![]() 长为_____;
长为_____;
(2)当AP⊥BD时,记此时点P为P0,点Q为Q0,移动点P的位置,求∠QQ0D的大小;
(3)在点P运动中,当以点Q为圆心,![]() BP为半径的圆与直线BD相切时,求BP的长度;
BP为半径的圆与直线BD相切时,求BP的长度;
(4)点P在线段BD上,由B向D运动过程(包含B、D两点)中,求CQ的取值范围,直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
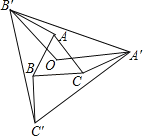
【题目】如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB′、BC′、CA′,连接A′B′、B′C′、A′C′、OA′、OB′.(1)∠A′OB′=___°;(2)当α=___°时,△A′B′C′的周长最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
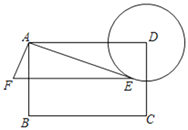
【题目】如图,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,使∠EAF=90°,tan∠AEF=![]() ,则点F与点C的最小距离为_____.
,则点F与点C的最小距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形ABCD折叠,使点C与点D重合于正方形内点P处,折痕分别为AF、BE,如果正方形ABCD的边长是2,那么△EPF的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com