
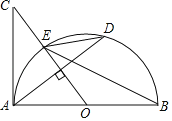
【题目】如图,AB是半圆O的直径,D为半圆上的一个动点(不与点A,B重合),连接AD,过点O作AD的垂线,交半圆O的切线AC于点C,交半圆O于点E.连接BE,DE.
(1)求证:∠BED=∠C.
(2)连接BD,OD,CD.
填空:
①当∠ACO的度数为 时,四边形OBDE为菱形;
②当∠ACO的度数为 时,四边形AODC为正方形.
【答案】(1)证明见解析;(2)①30°;②45°.
【解析】
(1)利用同角的余角相等证明∠BED=∠C;
(2)①当∠ACO=30°时,四边形OBDE是菱形,利用邻边相等的平行四边形为菱形进行证明;
②当∠ACO=45°时,四边形AODC是正方形,利用利用邻边相等的矩形为正方形进行证明.
(1)r如图,设AD,OC交于点P,
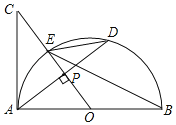
∵OC⊥AD,
∴∠APC=90°.
∴∠C+∠CAP=180°﹣∠APC=90°
∵AC是半圆O的切线,
∴∠CAO=∠CAP+∠BAD=90°.
∴∠BAD=∠C,
∵∠BED=∠BAD,
∴∠BED=∠C;
(2)①当∠ACO=30°时,四边形OBDE是菱形,理由如下
连接BD,如图

∵AB是半圆O的直径,
∴∠ADB=90°,
∵∠DAB=∠ACO=30°,
∴∠DBA=60°,
∵OE⊥AD,
∴![]() =
=![]()
∴∠DBE=∠ABE=30°
∵∠DEB=∠DAB=30°,
∴∠DEB=∠ABE,
DE∥AB
∵∠ADB=90°,即BD⊥AD,
OE⊥AD,
∴OE∥BD,
故四边形OBDE 是平行四边形
∵OB=OE
∴四边形OBDE 是菱形;
故答案为30°;
②当∠ACO=45°时,四边形AODC是正方形.理由如下
连接CD、OD,
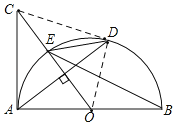
∵∠BED=∠ACO=45°,
∴∠BOD=2∠BED=90°,
∴∠AOD=90°,
∵OC⊥AD,
∴OC垂直平分AD
∴∠OCD=∠OCA=45°,
∴∠ACD=90°,
∵∠ACO=90°,
∴四边形AODC是矩形
∵OA=OD,
∴四边形AODC是正方形,
故答案为45°.


科目:初中数学 来源: 题型:
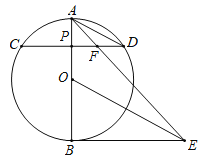
【题目】如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE交CD于F点.
(1)求证:DE为⊙O切线;
(2)若⊙O的半径为3,sin∠ADP=![]() ,求AD;
,求AD;
(3)请猜想PF与FD的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
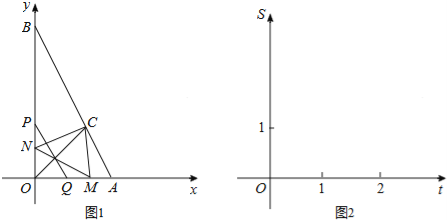
【题目】如图1,已知点A(2,0),B(0,4),∠AOB的平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P、Q关于直线OC的对称点M、N.设P运动的时间为t(0<t<2)秒.
(1)求C点的坐标,并直接写出点M、N的坐标(用含t的代数式表示);
(2)设△MNC与△OAB重叠部分的面积为S.
①试求S关于t的函数关系式;
②在图2的直角坐标系中,画出S关于t的函数图象,并回答:S是否有最大值?若有,写出S的最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为8cm,宽为6cm的长方形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与长方形的一个顶点重合,其余的两个顶点在长方形的边上).则剪下的等腰三角形的底边长可以是_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设k≠0,若函数y1=kx+3,y2=(x﹣k)2+k和y3=(x+k)2﹣k的图象与y轴依次交于A,B和C三点,设函数y2,y3的图象的顶点分别为D,E.
(1)当k=1时,请在直角坐标系中,分别画出函数y1,y2,y3的草图,并根据图象,写出你发现的两条结论;
(2)BC长与k之间是正比例函数关系吗?请作出判断,并说明理由;
(3)若△ADE的面积等于9,求y2随x的增大而减小时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
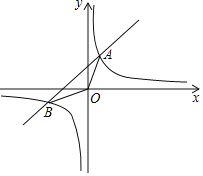
【题目】如图,已知一次函数y=kx+b(k≠0)与反比例函数y=![]() (m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w).
(m≠0)的图象相交于A、B两点,且点A的坐标是(1,2),点B的坐标是(﹣2,w).
(1)求一次函数与反比例函数的解析式;
(2)在x轴的正半轴上找一点C,使△AOC的面积等于△ABO的面积,并求出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现在平均每天比原计划多生产 50 台机器,现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同.
(1)现在平均每天生产多少台机器;
(2)生产 3000 台机器,现在比原计划提前几天完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
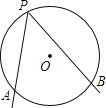
【题目】如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(1)已知∠APB是⊙O上关于点A、B的滑动角,
①若AB是⊙O的直径,则∠APB= °;
②若⊙O的半径是1,AB=![]() ,求∠APB的度数;
,求∠APB的度数;
(2)已知O2是⊙O1外一点,以O2为圆心作一个圆与⊙O1相交于A、B两点,∠APB是⊙O1上关于点A、B的滑动角,直线PA、PB分别交⊙O2于M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com