
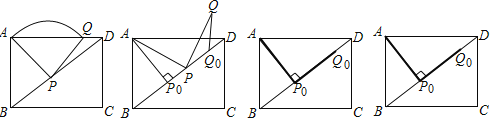
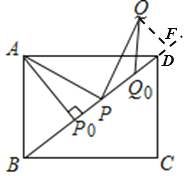
【题目】如图,在矩形ABCD中,AB=3,AD=4,P沿射线BD运动,连接AP,将线段AP绕点P顺时针旋转90°得线段PQ.
(1)当点Q落到AD上时,∠PAB=____°,PA=_____,![]() 长为_____;
长为_____;
(2)当AP⊥BD时,记此时点P为P0,点Q为Q0,移动点P的位置,求∠QQ0D的大小;
(3)在点P运动中,当以点Q为圆心,![]() BP为半径的圆与直线BD相切时,求BP的长度;
BP为半径的圆与直线BD相切时,求BP的长度;
(4)点P在线段BD上,由B向D运动过程(包含B、D两点)中,求CQ的取值范围,直接写出结果.
【答案】(1)45,![]() ,
,![]() π;(2)满足条件的∠QQ0D为45°或135°;(3)BP的长为
π;(2)满足条件的∠QQ0D为45°或135°;(3)BP的长为![]() 或
或![]() ;(4)
;(4)![]() ≤CQ≤7.
≤CQ≤7.
【解析】
(1)由已知,可知△APQ为等腰直角三角形,可得∠PAB,再利用三角形相似可得PA,及弧AQ的长度;
(2)分点Q在BD上方和下方的情况讨论求解即可.
(3)分别讨论点Q在BD上方和下方的情况,利用切线性质,在由(2)用BP0表示BP,由射影定理计算即可;
(4)由(2)可知,点Q在过点Qo,且与BD夹角为45°的线段EF上运动,有图形可知,当点Q运动到点E时,CQ最长为7,再由垂线段最短,应用面积法求CQ最小值.
解:(1)如图,过点P做PE⊥AD于点E
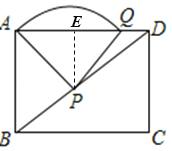
由已知,AP=PQ,∠APQ=90°
∴△APQ为等腰直角三角形
∴∠PAQ=∠PAB=45°
设PE=x,则AE=x,DE=4﹣x
∵PE∥AB
∴△DEP∽△DAB
∴![]() =
=![]()
∴![]() =
=![]()
解得x=![]()
∴PA=![]() PE=
PE=![]()
∴弧AQ的长为![]() 2π
2π![]() =
=![]() π.
π.
故答案为:45,![]() ,
,![]() π.
π.
(2)如图,过点Q做QF⊥BD于点F
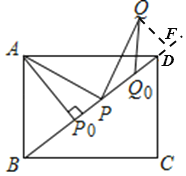
由∠APQ=90°,
∴∠APP0+∠QPD=90°
∵∠P0AP+∠APP0=90°
∴∠QPD=∠P0AP
∵AP=PQ
∴△APP0≌△PQF
∴AP0=PF,P0P=QF
∵AP0=P0Q0
∴Q0D=P0P
∴QF=FQ0
∴∠QQ0D=45°.
当点Q在BD的右下方时,同理可得∠PQ0Q=45°,
此时∠QQ0D=135°,
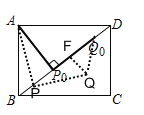
综上所述,满足条件的∠QQ0D为45°或135°.
(3)如图当点Q直线BD上方,当以点Q为圆心,![]() BP为半径的圆与直线BD相切时
BP为半径的圆与直线BD相切时
过点Q做QF⊥BD于点F,则QF=![]() BP
BP
由(2)可知,PP0=![]() BP
BP
∴BP0=![]() BP
BP
∵AB=3,AD=4
∴BD=5
∵△ABP0∽△DBA
∴AB2=BP0BD
∴9=![]() BP×5
BP×5
∴BP=![]()
同理,当点Q位于BD下方时,可求得BP=![]()
故BP的长为![]() 或
或![]()
(4)由(2)可知∠QQ0D=45°
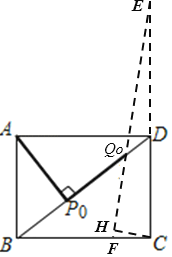
则如图,点Q在过点Q0,且与BD夹角为45°的线段EF上运动,
当点P与点B重合时,点Q与点F重合,此时,CF=4﹣3=1
当点P与点D重合时,点Q与点E重合,此时,CE=4+3=7
∴EF=![]() =
=![]() =5
=5![]()
过点C做CH⊥EF于点H
由面积法可知
CH=![]() =
=![]() =
=![]()
∴CQ的取值范围为:![]() ≤CQ≤7
≤CQ≤7


科目:初中数学 来源: 题型:
【题目】设k≠0,若函数y1=kx+3,y2=(x﹣k)2+k和y3=(x+k)2﹣k的图象与y轴依次交于A,B和C三点,设函数y2,y3的图象的顶点分别为D,E.
(1)当k=1时,请在直角坐标系中,分别画出函数y1,y2,y3的草图,并根据图象,写出你发现的两条结论;
(2)BC长与k之间是正比例函数关系吗?请作出判断,并说明理由;
(3)若△ADE的面积等于9,求y2随x的增大而减小时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校图书馆为了满足同学们阅读课外书的需求,计划购进甲、乙两种图书共100套,其中甲种图书每套120元,乙种图书每套80元.设购买甲种图书的数量![]() 套.
套.
(1)按计划用11000元购进甲、乙两种图书时,问购进这甲、乙两种图书各多少套?
(2)若购买甲种图书的数量要不少于乙种图书的数量的![]() ,购买两种图书的总费用为
,购买两种图书的总费用为![]() 元,求出最少总费用.
元,求出最少总费用.
(3)图书馆在不增加购买数量的情况下,增加购买丙种图书,要求甲种图书与丙种图书的购买费用相同.丙种图书每套100元,总费用比(2)中最少总费用多出1240元,请直接写出购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了_____名学生,最喜欢用电话沟通的所对应扇形的圆心角是____°;
(2)将条形统计图补充完整;
(3)运用这次的调查结果估计1200名学生中最喜欢用QQ进行沟通的学生有多少名?
(4)甲、乙两名同学从微信,QQ,电话三种沟通方式中随机选了一种方式与对方联系,请用列表或画树状图的方法求出甲乙两名同学恰好选中同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
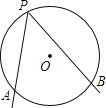
【题目】如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(1)已知∠APB是⊙O上关于点A、B的滑动角,
①若AB是⊙O的直径,则∠APB= °;
②若⊙O的半径是1,AB=![]() ,求∠APB的度数;
,求∠APB的度数;
(2)已知O2是⊙O1外一点,以O2为圆心作一个圆与⊙O1相交于A、B两点,∠APB是⊙O1上关于点A、B的滑动角,直线PA、PB分别交⊙O2于M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为有效利用电力资源,某市电力局采用“峰谷”用电政策,每天8:00﹣22:00为“峰时段”,22:00至次日8:00为“谷时段”.嘉淇家使用的是峰谷电价,他将家里2018年1月至5月的峰时段和谷时段用电量绘制成如图所示的条形统计图,已知嘉淇家1月份电费为51.8元,2月份电费为50.85元.
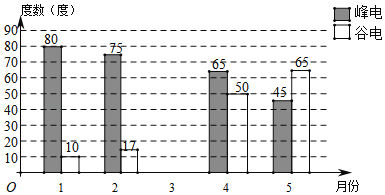
(1)“峰电”每度 元,“谷电”每度 ;
(2)嘉淇家3月份用电量比这5个月的平均用电量少1度,且3月份所交电费为49.54元,则3月份“峰电”度数为 度;
(3)2018年6月,嘉淇单位决定给职工补贴前五个月中的两个月份的电费,求恰好选中3月份和4月份的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆;两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计,EF长度远大于车辆宽度),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=AE=1.2米,该地下车库出口的车辆限高标志牌设置如图4是否合理?请通过计算说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线C1:y=﹣(x+m)2+m2(m>0),抛物线C2:y=(x﹣n)2+n2(n>0),称抛物线C1,C2互为派对抛物线,例如抛物线C1:y=﹣(x+1)2+1与抛物线C2:y=(x﹣![]() )2+2是派对抛物线,已知派对抛物线C1,C2的顶点分别为A,B,抛物线C1的对称轴交抛物线C2于C,抛物线C2的对称轴交抛物线C1与D.
)2+2是派对抛物线,已知派对抛物线C1,C2的顶点分别为A,B,抛物线C1的对称轴交抛物线C2于C,抛物线C2的对称轴交抛物线C1与D.
(1)已知抛物线①y=﹣x2﹣2x,②y=(x﹣3)2+3,③y=(x﹣![]() )2+2,④y=x2﹣x+
)2+2,④y=x2﹣x+![]() ,则抛物线①②③④中互为派对抛物线的是 (请在横线上填写抛物线的数字序号);
,则抛物线①②③④中互为派对抛物线的是 (请在横线上填写抛物线的数字序号);
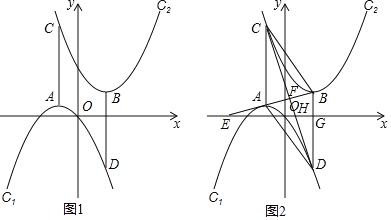
(2)如图1,当m=1,n=2时,证明AC=BD;
(3)如图2,连接AB,CD交于点F,延长BA交x轴的负半轴于点E,记BD交x轴于G,CD交x轴于点H,∠BEO=∠BDC.
①求证:四边形ACBD是菱形;
②若已知抛物线C2:y=(x﹣2)2+4,请求出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com