
 如图,在等边三角形ABC中,AD是高,点G为AD的中点,过G作EF∥AC交AB于点F,交CD于点E,下列说法正确的有①③④(将你认为正确选项的序号都填上).
如图,在等边三角形ABC中,AD是高,点G为AD的中点,过G作EF∥AC交AB于点F,交CD于点E,下列说法正确的有①③④(将你认为正确选项的序号都填上).分析 先根据等边三角形的性质得出∠DAC=30°,再由平行线的性质可得出∠AGF的度数;设AC=a,由直角三角形的性质求出AD的长,再由EF∥AC,G是AD的中点可求出EF的长,故可得出②错误;根据三角形中位线定理求出EG的长,进而可得出EG的长,得出③正确;过点F作FH∥BC,根据相似三角形的性质可得出FH=$\frac{1}{2}$DE,由三角形的面积公式可知④正确.
解答  解:∵△ABC是等边三角形,AD⊥BC,
解:∵△ABC是等边三角形,AD⊥BC,
∴∠DAC=30°.
∵EF∥AC,
∴∠AGF=∠DAC=30°,故①正确;
设AC=a,
∵∠DAC=30°,
∴AD=AC•cos30°=$\frac{\sqrt{3}}{2}$a;
∵点G为AD的中点,
∴GE是△ADC的中位线,
∴点E时CD的中点,
∴EF=$\frac{3}{4}$AC=$\frac{3}{4}$a,
∴AD≠EF,故②错误;
∵EF=$\frac{3}{4}$AC=$\frac{3}{4}$a,GE=$\frac{1}{2}$AC=$\frac{1}{2}$a,
∴EG=2FG,故③正确;
过点F作FH∥BC,
∵AH∥DE,
∴△FGH∽△EGD.
∵EG=$\frac{1}{2}$FG,
∴FH=$\frac{1}{2}$DE.
∵AG=GD,
∴S△GDE=2S△AFG,故④正确.
故答案为:①③④.
点评 本题考查的是三角形中位线定理,根据题意作出辅助线,构造出相似三角形是解答此题的关键.


科目:初中数学 来源: 题型:填空题
 如图,给一幅长8m,宽5m的矩形风景画(图中阴影部分)镶一个画框,若设画框的宽均为xm,装好画框后总面积为70m2,则根据题意可列方程为(8+2x)(5+2x)=70.
如图,给一幅长8m,宽5m的矩形风景画(图中阴影部分)镶一个画框,若设画框的宽均为xm,装好画框后总面积为70m2,则根据题意可列方程为(8+2x)(5+2x)=70.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{7}{12}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
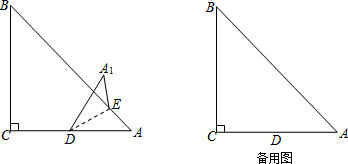
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在钝角△ABC中,AC<BC,用尺规在BC上确定一点P,使PA+PC=BC,下面是四个同学的作法(只留下了作图痕迹,未连接PA),其中正确的是( )
如图,在钝角△ABC中,AC<BC,用尺规在BC上确定一点P,使PA+PC=BC,下面是四个同学的作法(只留下了作图痕迹,未连接PA),其中正确的是( )| A. | 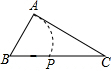 | B. | 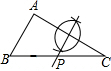 | C. | 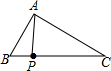 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com