
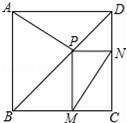
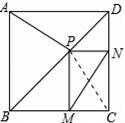
如图,点P是正方形ABCD的对角线BD上的一点,PM⊥BC,PN⊥CD,垂足分别为点M,N.求证:AP=MN.

【考点】全等三角形的判定与性质;矩形的判定与性质;正方形的性质.
【专题】证明题.
【分析】连接PC,根据正方形的性质可得∠BCD=90°,∠ABD=∠CBD=45°,AB=BC,然后求出四边形PMCN是矩形,根据矩形的对角线相等可得PC=MN,再利用“边角边”证明△ABP和△CBP全等,根据全等三角形对应边相等可得AP=PC,从而得解.
【解答】解:连接PC,
∵四边形ABCD为正方形,
∴∠BCD=90°,∠ABD=∠CBD=45°,AB=BC,
又∵PN⊥DC,PM⊥BC,
∴∠PMC=90°,∠PNC=90°,
∴四边形PMCN为矩形,
∴PC=MN,
在△ABP和△CBP中,

 ,
,
∴△ABP≌△CBP(SAS),
∴AP=PC,
∴AP=MN.

【点评】本题考查了正方形的性质,全等三角形的判定与性质,矩形的判定与性质,作出辅助线,构造出全等三角形是解题的关键.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
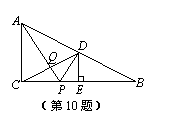
如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是………………………………………………………………( )
 A.AQ=
A.AQ= 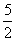 PQ B.AQ=3PQ C.AQ=
PQ B.AQ=3PQ C.AQ= 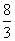 PQ D.AQ=4PQ
PQ D.AQ=4PQ
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图,直线CD与直线AB相交于C,根据下列语句画图
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,将三角形各点的横坐标都减去3,纵坐标保持不变,所得图形与原图形相比( )
A.向右平移了3个单位 B.向左平移了3个单位
C.向上平移了3个单位 D.向下平移了3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
已知,如图,正方形ABCD,菱形EFGP,点E、F、G分别在AB、AD、CD上,延长DC,PH⊥DC于H.
(1)求证:GH=AE;
(2)若菱形EFGP的周长为20cm,
 ,FD=2,求△PGC的面积.
,FD=2,求△PGC的面积.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com