
.如图,直线CD与直线AB相交于C,根据下列语句画图
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
如图,反比例函数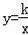
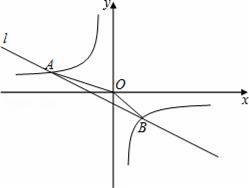
 (k≠0,k为常数)的图象与一次函数y=ax+b(a≠0,a、b为常数)的图象相交于A(﹣4,1)、B(2,m)两点.
(k≠0,k为常数)的图象与一次函数y=ax+b(a≠0,a、b为常数)的图象相交于A(﹣4,1)、B(2,m)两点.
(1)求k、m的值;
(2)求△AOB的面积;
(3)根据图象直接写出使不等式ax+b>
 成立的x的取值范围.
成立的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
小明家所在学校离家距离为2千米,某天他放学后骑自行车回家,行使了5分钟后,因故停留10分钟,继续骑了5分钟到家、下面哪一个图象能大致描述他回家过程中离学校的距离S(千米)与所用时间t(分)之间的关系( )
A.
 B.
B.

C.
 D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
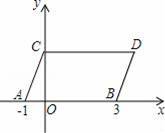
如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A、B 的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com