
如图,反比例函数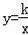
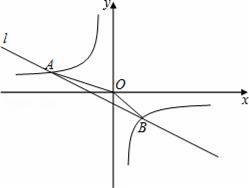
 (k≠0,k为常数)的图象与一次函数y=ax+b(a≠0,a、b为常数)的图象相交于A(﹣4,1)、B(2,m)两点.
(k≠0,k为常数)的图象与一次函数y=ax+b(a≠0,a、b为常数)的图象相交于A(﹣4,1)、B(2,m)两点.
(1)求k、m的值;
(2)求△AOB的面积;
(3)根据图象直接写出使不等式ax+b>
 成立的x的取值范围.
成立的x的取值范围.

【考点】反比例函数与一次函数的交点问题.
【分析】(1)将A坐标代入反比例解析式求出m的值,确定出反比例解析式,将B坐标代入反比例解析式求n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)设一次函数与x轴交于C点,求出C坐标,确定出OC的长,三角形AOB面积=三角形AOC面积+三角形BOC面积,求出即可.
(3)根据图象和交点坐标找出一次函数图象位于反比例函数图象上方时x的范围即可.
【解答】解:(1)将A(﹣4,1)代入反比例解析式得:k=﹣4×1=﹣4,
则反比例解析式为y=﹣
 ;
;
将B(2,m)代入反比例解析式得:m=﹣2,即B(2,﹣2),
将A与B坐标代y=ax+b中,得: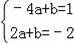
 ,
,
解得:
 .
.
则一次函数解析式为y=﹣
 x﹣1;
x﹣1;
(2)设一次函数与x轴交于点C,
对于一次函数y=﹣
 x﹣1,令y=0,得到x=﹣2,即OC=2,
x﹣1,令y=0,得到x=﹣2,即OC=2,
则S△AOB=S△AOC+S△BOC=
 ×2×1+
×2×1+
 ×2×2=3.
×2×2=3.
(3)由图象得:不等式ax+b>
 成立的x的取值范围为0<x<2或x<﹣4.
成立的x的取值范围为0<x<2或x<﹣4.
【点评】此题考查了一次函数与反比例函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,利用了数形结合的思想,熟练掌握待定系数法是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
某工厂接受了20天内生产1200台GH型电子产品的总任务. 已知每台GH型产品由4个G型装置和3个H型装置配套组成. 工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?
(2)为了在规定期限内完成总任务, 工厂决定补充一些新工人,这些新工人只能独立进行G 型装置的加工,且每人每天只能加工4个G型装置. 请问至少需要补充多少名新工人?
工厂决定补充一些新工人,这些新工人只能独立进行G 型装置的加工,且每人每天只能加工4个G型装置. 请问至少需要补充多少名新工人?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是………………………………………………………………( )
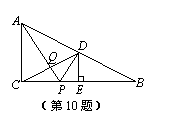 A.AQ=
A.AQ= 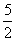 PQ B.AQ=3PQ C.AQ=
PQ B.AQ=3PQ C.AQ= 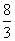 PQ D.AQ=4PQ
PQ D.AQ=4PQ
查看答案和解析>>
科目:初中数学 来源: 题型:
.如图,直线CD与直线AB相交于C,根据下列语句画图
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com