
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED; ②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED; ②FG=2;③tan∠E=![]() ; ④S△DEF=4
; ④S△DEF=4![]() ,其中正确的是( )
,其中正确的是( )

A. ①②③ B. ①②④ C. ②③④ D. ①②③④
【答案】B
【解析】
由垂径定理得出CG=DG,![]() ,得出圆周角∠ADF=∠E,再由公共角相等,即可得出△ADF∽△AED,①正确;
,得出圆周角∠ADF=∠E,再由公共角相等,即可得出△ADF∽△AED,①正确;
由已知条件求出FD,得出CD、CG,即可求出FG=2,②正确;
由相交弦定理求出EF,得出AE,由△ADF∽△AED,得出对应边成比例![]() ,求出AD2=21,由勾股定理求出AG,得出tan∠E=tan∠ADF=
,求出AD2=21,由勾股定理求出AG,得出tan∠E=tan∠ADF=![]() ,③错误;
,③错误;
作EM⊥CD于M,则EM∥AB,证出△EFM∽△AFG,得出比例式![]() ,求出ME,即可得出S△DEF=
,求出ME,即可得出S△DEF=![]() FDME=4
FDME=4![]() ,④正确.
,④正确.
∵AB是⊙O的直径,弦CD⊥AB,
∴CG=DG,![]() ,∠AGF=∠AGD=90°,
,∠AGF=∠AGD=90°,
∴∠ADF=∠E,
又∵∠DAF=∠EAD,
∴△ADF∽△AED,
∴①正确;
∵![]() ,CF=2,
,CF=2,
∴FD=6,
∴CD=8,
∵CG=DG,
∴CG=DG=4,
∴FG=2,
∴②正确;
∵AFEF=CFFD,
即3EF=2×6,
∴EF=4,
∴AE=7,
∵△ADF∽△AED,
∴![]() ,
,
∴AD2=AE×AF=7×3=21,
在Rt△ADG中,AG=![]() ,
,
∴tan∠E=tan∠ADF=![]() ,
,
∴③错误;
作EM⊥CD于M,如图所示:

则EM∥AB,
∴△EFM∽△AFG,
∴![]() ,
,![]()
∴ME=![]() ,
,
∴S△DEF=![]() FDME=
FDME=![]() ×6×
×6×![]() =4
=4![]() ,
,
∴④正确;
故选B.


科目:初中数学 来源: 题型:
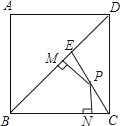
【题目】如图,边长为1的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七(一)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据整理如下表(部分):
月均用水量x/m3 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 | x>20 |
频数/户 | 12 | 20 | 3 | ||
频率 | 0.12 | 0.07 |
若该小区有800户家庭,据此估计该小区月均用水量不超过10m3的家庭约有________户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=10,BC=12,E为DC的中点,连接BE,作AF⊥BE,垂足为F.
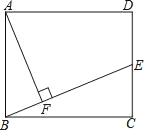
(1)求证:△BEC∽△ABF;
(2)求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆 O 的半径为 1,过点 A(2,0)的直线与圆 O 相切于点 B,与 y 轴相交于点 C.
(1)求 AB 的长;
(2)求直线 AB 的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
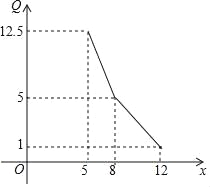
【题目】某专卖店经市场调查得知,一种商品的月销售量 Q(单位:吨)与销售价格 x(单位:万元/吨)的关系可用下图中的折线表示.
(1)写出月销售量 Q 关于销售价格 x 的关系;
(2)如果该商品的进价为 5 万元/吨,除去进货成本外,专卖店销售该商品每月的固定成本为 10 万元,问该商品 每吨定价多少万元时,销售该商品的月利润最大?并求月利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
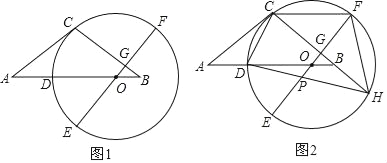
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是![]() 的中点.
的中点.
(1)求证:AC是⊙O的切线;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
(3)在(2)的条件下,连接CD,若tan∠HDC=![]() ,CG=4,求OP的长.
,CG=4,求OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
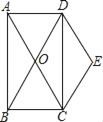
【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com