
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,5秒后,两点相距15个单位长度.已知点B的速度是点A的速度的2倍(速度单位:单位长度/秒).
(1)求出点A,点B运动的速度,并在数轴上标出A,B两点从原点出发运动5秒时的位置; ![]()
(2)若A,B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,再过几秒时,原点恰好处在点A,点B的正中间?
(3)若A,B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从原点O位置出发向B点运动,且C的速度是点A的速度的一半;当C运动几秒后,C为AB的中点?
【答案】
(1)解:设A的速度是x,则B的速度为2x,由题意,得
5(x+2x)=15,
解得:x=1,
∴B的速度为2,
∴A到达的位置为﹣5,B到达的位置是10,在数轴上的位置如图:
![]()
答:A的速度为1;B的速度为2
(2)解:设y秒后,原点恰好在A、B的正中间,由题意,得
10﹣2y=y+5,
y= ![]() .
.
答:再过 ![]() 秒时,原点恰好处在点A、点B的正中间
秒时,原点恰好处在点A、点B的正中间
(3)解:设当C运动z秒后,C为AB的中点,由题意得
﹣ ![]() z=
z= ![]() (﹣5﹣z+10﹣2z),
(﹣5﹣z+10﹣2z),
解得:z=2.5.
答:当C运动2.5秒后,C为AB的中点
【解析】(1)设A的速度是x,则B的速度为4x,根据行程问题的数量关系建立方程求出其解即可;(2)设y秒后,原点恰好在A、B的正中间,根据两点到原点的距离相等建立方程求出其解即可;(3)设当C运动z秒后,C为AB的中点,由中点坐标公式就可以求出结论.


科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施. 经调查发现,每件商品每降价1元,商场平均每天可多售出 2件.据此规律计算:每件商品降价元时,商场日盈利可达到2100元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
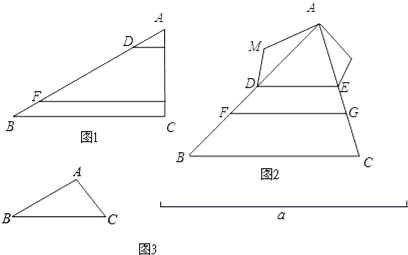
【题目】【回归课本】我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
(1)如图1,在△ABC中,点D、F在AB上,E、G在AC上,DE∥FC∥BC.若AD=2,AE=1,DF=6,则EG= , ![]() = .
= .
(2)如图2,在△ABC 中,点D、F在AB上,E、G在AC上,且DE∥BC∥FG.以AD、DF、FB为边构造△ADM(即AM=BF,MD=DF);以AE、EG、GC为边构造△AEN(即AN=GC,NE=EG).
求证:∠M=∠N.
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题:
(3)如图3,已知△ABC和线段a,请用直尺与圆规作△A′B′C′.
满足:①△A′B′C′∽△ABC;②△A′B′C′的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象交反比例函数![]() (x>0)图象于点A、B,交x轴于点C.
(x>0)图象于点A、B,交x轴于点C.
(1)求m得取值范围;
(2)若点A的坐标是(2,﹣4),且![]() ,求m的值和一次函数的解析式.
,求m的值和一次函数的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com