
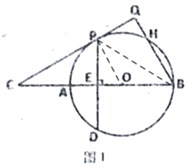
【题目】已知:如图,AB为⊙O的直径,C是BA延长线上一点,CP切⊙O于P,弦PD⊥AB于E,过点B作BQ⊥CP于Q,交⊙O于H.
(1)如图1,求证:PQ=PE;
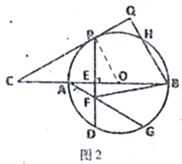
(2)如图2,G是圆上一点,∠GAB=30![]() ,连接AG交PD于F,连接BF,tan∠BFE=
,连接AG交PD于F,连接BF,tan∠BFE=![]() ,求∠C的度数;
,求∠C的度数;
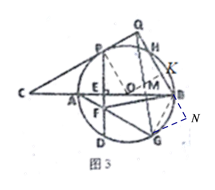
(3)如图3,在(2)的条件下,PD=6![]() ,连接QG交BC于点M,求QM的长.
,连接QG交BC于点M,求QM的长.

【答案】(1)证明见解析(2)30°(3) QM=![]()
【解析】试题分析:
(1)连接OP,PB,由已知易证∠OBP=∠OPB=∠QBP,从而可得BP平分∠OBQ,结合BQ⊥CP于点Q,PE⊥AB于点E即可由角平分线的性质得到PQ=PE;
(2)如下图2,连接OP,则由已知易得∠CPO=∠PEC=90°,由此可得∠C=∠OPE,设EF=x,则由∠GAB=30°,∠AEF=90°可得AE= ![]() ,在Rt△BEF中,由tan∠BFE=
,在Rt△BEF中,由tan∠BFE=![]() 可得BE=
可得BE= ![]() ,从而可得AB=
,从而可得AB= ![]() ,则OP=OA=
,则OP=OA= ![]() ,结合AE=
,结合AE= ![]() 可得OE=
可得OE= ![]() ,这样即可得到sin∠OPE=
,这样即可得到sin∠OPE=![]() ,由此可得∠OPE=30°,则∠C=30°;
,由此可得∠OPE=30°,则∠C=30°;
(3)如下图3,连接BG,过点O作OK⊥HB于点K,结合BQ⊥CP,∠OPQ=90°,可得四边形POKQ为矩形.由此可得QK=PO,OK∥CQ从而可得∠KOB=∠C=30°;由已知易证PE=![]() ,在Rt△EPO中结合(2)可解得PO=6,由此可得OB=QK=6;在Rt△KOB中可解得KB=3,由此可得QB=9;在△ABG中由已知条件可得BG=6,∠ABG=60°;过点G作GN⊥QB交QB的延长线于点N,由∠ABG=∠CBQ=60°,可得∠GBN=60°,从而可得解得GN=
,在Rt△EPO中结合(2)可解得PO=6,由此可得OB=QK=6;在Rt△KOB中可解得KB=3,由此可得QB=9;在△ABG中由已知条件可得BG=6,∠ABG=60°;过点G作GN⊥QB交QB的延长线于点N,由∠ABG=∠CBQ=60°,可得∠GBN=60°,从而可得解得GN=![]() ,BN=3,由此可得QN=12,则在Rt△BGN中可解得QG=
,BN=3,由此可得QN=12,则在Rt△BGN中可解得QG=![]() ,由∠ABG=∠CBQ=60°可知△BQG中BM是角平分线,由此可得QM:GM=QB:GB=9:6由此即可求得QM的长了.
,由∠ABG=∠CBQ=60°可知△BQG中BM是角平分线,由此可得QM:GM=QB:GB=9:6由此即可求得QM的长了.
试题解析:
(1)如下图1,连接OP,PB,∵CP切⊙O于P,
∴OP⊥CP于点P,
又∵BQ⊥CP于点Q,
∴OP∥BQ,
∴∠OPB=∠QBP,
∵OP=OB,
∴∠OPB=∠OBP,
∴∠QBP=∠OBP,
又∵PE⊥AB于点E,
∴PQ=PE;
(2)如下图2,连接![]() ,∵CP切⊙O于P,
,∵CP切⊙O于P,
∴![]()
∴![]()
∵PD⊥AB
∴![]()
∴![]()
∴![]()
在Rt![]() 中,∠GAB=30°
中,∠GAB=30°
∴设EF=x,则![]()
在Rt![]() 中,tan∠BFE=3
中,tan∠BFE=3![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴在Rt![]() PEO中,
PEO中, ![]()
∴![]() 30°;
30°;
(3)如下图3,连接BG,过点O作![]() 于K,又BQ⊥CP,
于K,又BQ⊥CP,
∴![]() ,
,
∴四边形POKQ为矩形,
∴QK=PO,OK//CQ,
∴![]() 30°,
30°,
∵⊙O 中PD⊥AB于E ,PD=6![]() ,AB为⊙O的直径,
,AB为⊙O的直径,
∴PE= ![]() PD= 3
PD= 3![]() ,
,
根据(2)得![]() ,在Rt
,在Rt![]() EPO中,
EPO中, ![]() ,
,
∴![]() ,
,
∴OB=QK=PO=6,
∴在Rt![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴QB=9,
在△ABG中,AB为⊙O的直径,
∴![]() AGB=90°,
AGB=90°,
∵![]() BAG=30°,
BAG=30°,
∴BG=6, ![]() ABG=60°,
ABG=60°,
过点G作GN⊥QB交QB的延长线于点N,则∠N=90°,∠GBN=180°-∠CBQ-∠ABG=60°,
∴BN=BQ·cos∠GBQ=3,GN=BQ·sin∠GBQ=![]() ,
,
∴QN=QB+BN=12,
∴在Rt△QGN中,QG=![]() ,
,
∵∠ABG=∠CBQ=60°,
∴BM是△BQG的角平分线,
∴QM:GM=QB:GB=9:6,
∴QM=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,延长AC至点D,使CD=BC,连接BD,作CE⊥AB于点E,DF⊥BC交BC的延长线于点F,且CE=DF.
(1)求证:AB=AC.
(2)如果∠ABD=105°,求∠A的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
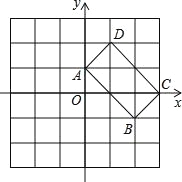
【题目】如图,在 6×6 的网格中,四边形 ABCD 的顶点都在格点上,每个格子都是边长为 1 的正方形,建立如图所示的平面直角坐标系.
(1)画出四边形 ABCD 关于 y 轴对称和四边形 A′B′C′D′(点 A、B、C、D的对称点分别是点 A′B′C′D′.
(2)求 A、B′、B、C 四点组成和四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知双曲线y=![]() (x<0)和y=
(x<0)和y=![]() (x>0),直线OA与双曲线y=
(x>0),直线OA与双曲线y=![]() 交于点A,将直线OA向下平移与双曲线y=
交于点A,将直线OA向下平移与双曲线y=![]() 交于点B,与y轴交于点P,与双曲线y=
交于点B,与y轴交于点P,与双曲线y=![]() 交于点C,S△ABC=6,
交于点C,S△ABC=6,![]() =
=![]() ,则k=( )
,则k=( )

A. ﹣6 B. ﹣4 C. 6 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项).下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)小龙一共抽取了 名学生.
(2)补全条形统计图;
(3)求“其他”部分对应的扇形圆心角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)分别写出以下顶点的坐标:A( , );B( , ) ;C( , ).
(2)顶点A关于x轴对称的点A′的坐标( , ),顶点C关于y轴对称的点C′的坐标( , ).
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
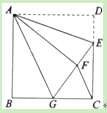
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以点M(6,8)为圆心,2为半径的圆上有一动点P,若A(﹣2,0),B(2,0),连接PA,PB,则当PA2+PB2取得最大值时,PO的长度为( )
A. 8 B. 10 C. 12 D. 10![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com