
【题目】已知抛物线![]() 的解析式为
的解析式为![]() ,(与
,(与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,项点为
,项点为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)若将抛物线![]() 沿着直线
沿着直线![]() 的方向平移得到抛物线
的方向平移得到抛物线![]() ;
;
①当抛物线![]() 与直线
与直线![]() 只有一个公共点时,求抛物线
只有一个公共点时,求抛物线![]() 的解析式;
的解析式;
②点![]() 是①中抛物线上一点,若
是①中抛物线上一点,若![]() 且
且![]() 为整数,求满足条件的点
为整数,求满足条件的点![]() 的个数.
的个数.
【答案】(1)点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() ;(2)①
;(2)①![]() ,②满足条件的
,②满足条件的![]() 点有
点有![]() 个.
个.
【解析】
(1)令y=0求出x,可得点A、B的坐标;令x=0求出y,可得点D的坐标;将二次函数的解析式化为顶点式即可得点P的坐标;
(2)①先求出直线PD的解析式,由抛物线![]() 的顶点在直线PD上移动可设出抛物线
的顶点在直线PD上移动可设出抛物线![]() 的顶点式,根据抛物线
的顶点式,根据抛物线![]() 与直线
与直线![]() 只有一个公共点,利用
只有一个公共点,利用![]() 可求得抛物线的顶点坐标,即可求得其解析式;
可求得抛物线的顶点坐标,即可求得其解析式;
②先求出当![]() 、
、![]() 时
时![]() 的取值,根据二次函数的顶点式及其图象性质可分别求得当
的取值,根据二次函数的顶点式及其图象性质可分别求得当![]() 、
、![]() 时
时![]() 的取值范围,进而得出
的取值范围,进而得出![]() 的整数值,即可求出满足条件的点
的整数值,即可求出满足条件的点![]() 的个数.
的个数.
解:(1)取![]() ,即
,即![]()
解得:![]()
则点![]() ,点
,点![]()
取![]() ,得
,得![]()
则点![]()
又![]()
则点![]()
(2)①设直线![]() 的解析式为
的解析式为![]()
![]() 点
点![]() ,点
,点![]()
![]()
解得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
![]() 抛物线
抛物线![]() 沿着直线
沿着直线 ![]() 的方向平移得到抛物线
的方向平移得到抛物线![]()
![]() 平移后
平移后![]() 的顶点坐标为
的顶点坐标为![]()
设平移后![]() 解析式为
解析式为![]()
又抛物线![]() 与直线
与直线![]() 只有一个公共点
只有一个公共点
令![]()
整理得:![]()
则![]() ,即
,即![]()
解得![]()
![]() 平移后所得抛物线
平移后所得抛物线![]() 的解析式为
的解析式为![]()
即![]()
②![]() 的顶点为
的顶点为![]()
∵当![]() 时,
时,![]() 时
时![]()
∴当![]() 时,
时,![]()
则![]() 有
有![]() 个整数
个整数
当![]() 时,
时,![]()
则![]() 有
有![]() 个整数
个整数
抛物线是连续的,所以![]() 可以取到当
可以取到当![]() 时的函数值的所有整数,
时的函数值的所有整数,
故满足条件的![]() 点有
点有![]() 个.
个.


科目:初中数学 来源: 题型:
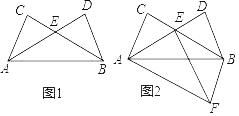
【题目】如图1,点C、D是线段AB同侧两点,且AC=BD,∠CAB=∠DBA,连接BC,AD交于点 E.
(1)求证:AE=BE;
(2)如图2,△ABF与△ABD关于直线AB对称,连接EF.
①判断四边形ACBF的形状,并说明理由;
②若∠DAB=30°,AE=5,DE=3,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长城公司为希望小学捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.
(1)下列事件是不可能事件的是
A.选购甲品牌的B型号;
B.选购甲品牌的C型号和乙品牌的D型号;
C.既选购甲品牌也选购乙品牌;
D.只选购乙品牌的E型号.
(2)用列表法或树状图法,写出所有的选购方案,若每种方案被选中的可能性相同,求A型号的器材被选中的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
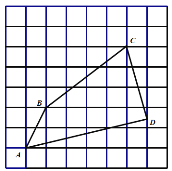
【题目】如图,在每个小正方形的边长为的网格中,点![]() 均在格点上,
均在格点上,![]() 为小正方形边中点.
为小正方形边中点.
(1)![]() 的长等于 ______;
的长等于 ______;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个点![]() ,使其满足
,使其满足![]() 说明点
说明点![]() 的位置是如何找到的(不要求证明)______.
的位置是如何找到的(不要求证明)______.
查看答案和解析>>
科目:初中数学 来源: 题型:
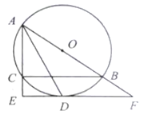
【题目】如图所示,![]() 是
是![]() 的外接圆,
的外接圆,![]() 为直径,
为直径,![]() 的平分线交O于点D,过点D作
的平分线交O于点D,过点D作![]() ,分别交
,分别交![]() ,
,![]() 的延长线于点E,F.
的延长线于点E,F.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)填空:
①当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 为菱形;
为菱形;
②若![]() 的半径为
的半径为![]() ,
,![]() ,则
,则![]() 的长为_________.
的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
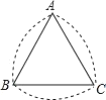
【题目】如图所示的曲边三角形可按下述方法作出:作等边三角形![]() ;分别以点
;分别以点![]() ,
,![]() ,
,![]() 为圆心,以
为圆心,以![]() 的长为半径作
的长为半径作![]() ,
,![]() ,
,![]() .三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为
.三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为![]() ,那么这个曲边三角形的面积是___________.
,那么这个曲边三角形的面积是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
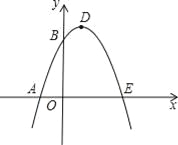
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张用4张相同的小纸条做成甲、乙、丙、丁4支签,放在一个盒子中,搅匀后先从盒子中任意抽出1支签(不放回),再从剩余的3支签中任意抽出1支签.
(1)小张第一次抽到的是乙签的概率是 ;
(2)求抽出的两支签中,1支为甲签、1支为丙签的概率(用画树状图或列表法求解).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com