
����Ŀ����ͼ����֪���κ���y=ax2+bx+c����A����1��0����B��3��0����N��2��3�����㣬����y�ύ�ڵ�C��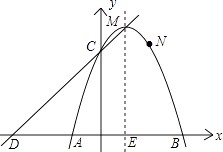
��1����������κ����Ľ���ʽ����д������M����C�����ꣻ
��2����ֱ��y=kx+d����C��M���㣬����x�ύ�ڵ�D����֤���ı���CDAN��ƽ���ı��Σ�
��3����P��������κ����ĶԳ�����һ���㣬��̽�����Ƿ���������ĵ�P��ʹ�Ե�PΪԲ�ĵ�Բ����A��B���㣬������ֱ��CD���У�������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��Ϊ���κ���y=ax2+bx+c��ͼ����A����1��0����B��3��0����N��2��3��
���ԣ��ɽ��������飺 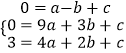 ����ã�
����ã� ![]()
���ԣ�������κ����Ľ���ʽΪy=��x2+2x+3��
���ԣ�����M��1��4������C��0��3��
��2��
�⣺ֱ��y=kx+d����C��M���㣬
���� ![]() ��
��
��k=1��d=3��
ֱ�߽���ʽΪy=x+3��
��y=0����x=��3��
��D����3��0��
��CD= ![]() ��AN=
��AN= ![]() ��AD=2��CN=2
��AD=2��CN=2
��CD=AN��AD=CN��2�֣�
���ı���CDAN��ƽ���ı���
��3��
�⣺������������ĵ�P��ʹ�Ե�PΪԲ�ĵ�Բ����A��B���㣬������ֱ��CD���У�
��Ϊ������κ����ĶԳ�����ֱ��x=1��
�ʿ���P��1��y0����
��PA��Բ�İ뾶��PA2=y02+22��
��P��ֱ��CD�Ĵ��ߣ�����ΪQ����PQ=PAʱ��PΪԲ�ĵ�Բ��ֱ��CD���У�
�ɵڣ�2��С���ã���MDEΪ����ֱ�������Σ�
�ʡ�PQMҲ�ǵ���ֱ�������Σ�
��P��1��y0����PE=y0��PM=|4��y0|�� ![]() ��
��
��PQ2=PA2�÷��̣� ![]() ��
��
��� ![]() ���������⣬
���������⣬
���ԣ���������ĵ�P���ڣ�������Ϊ��1�� ![]() ����1��
����1�� ![]() ��
��
����������1���������⽫��A��B��N��������뺯������ʽ����ɷ����鼴����ã���2����õ�C��M�����꣬�ɵ�ֱ��CM�Ľ���ʽ������õ�D�����꣬���ɵõ�CD= ![]() ��AN=
��AN= ![]() ��AD=2��CN=2������ƽ���ı��ε��ж������ɵ��ı���CDAN��ƽ���ı��Σ���3��������������ĵ�P��ʹ�Ե�PΪԲ�ĵ�Բ����A��B���㣬������ֱ��CD���У���Ϊ������κ����ĶԳ�����ֱ��x=1���ʿ���P��1��y0������PA��Բ�İ뾶��PA2=y02+22 ��
��AD=2��CN=2������ƽ���ı��ε��ж������ɵ��ı���CDAN��ƽ���ı��Σ���3��������������ĵ�P��ʹ�Ե�PΪԲ�ĵ�Բ����A��B���㣬������ֱ��CD���У���Ϊ������κ����ĶԳ�����ֱ��x=1���ʿ���P��1��y0������PA��Բ�İ뾶��PA2=y02+22 ��
��P��ֱ��CD�Ĵ��ߣ�����ΪQ����PQ=PAʱ��PΪԲ�ĵ�Բ��ֱ��CD���У�
�ɵڣ�2��С���ã���MDEΪ����ֱ�������Σ��ʡ�PQMҲ�ǵ���ֱ�������Σ��̶������������ĵ�P���ڣ�������Ϊ��1�� ![]() ����1��
����1�� ![]() ����
����
�����㾫����������Ŀ����֪���������ö��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУѧ������������������ȡ��У������Ů�����г������飮��֪��ȡ�������У�������Ů����������ͬ�������������ݻ�������ͳ��ͼ������A�飺x��155�� B�飺155��x��160�� C�飺160��x��165�� D��165��x��170��E�飺x��170�� 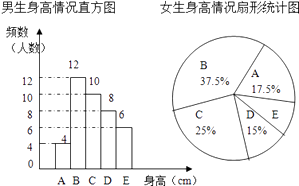
����ͼ���ṩ����Ϣ���ش��������⣺
��1�������У������������������飬��λ�����飮
��2�������У�Ů����������E����������ˣ�
��3����֪��У��������400�ˣ�Ů��380�ˣ������������160��x��170֮���ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����45���ǵ����ǰ��ֱ�Ƕ������һ�ſ�Ϊ3cm��ֽ�������ϣ���һ����
����ֽ������һ�����ϣ�������ǰ��һ����ֽ����һ�����ڵ�ֱ�߳�30���ǣ���ͼ��3����
�����ǰ�����ߵij�Ϊ�� ��
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������ABCD�У�AB��DC��BD��AD��AD=DC=BC=2cm����ô����ABCD������� �� 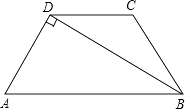
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ���ֵ��1+2+22+23+24++22013��
�⣺��S=1+2+22+23+24+��+22013������ʽ����ͬʱ����2����
2S=2+22+23+24+��+22013+22014
����ʽ��ȥ��ʽ����2S��S=22014��1��
��S=1+2+22+23+24++22013=22014��1��
������մ˷�����1+3+32+33+34+��+32018��ֵ�ǣ�������
A. 32018��1 B. ![]() C. 32019��1 D.
C. 32019��1 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧÿ�����������ڹ涨ʱ���ѧУ���ţ����꼶ͬѧС��ÿ������ͬһʱ��Ӽ������г���ѧУ������һ��������ÿСʱ15ǧ���ٶȵ�У�������У�ſڵ���6���Ӳſ��ţ����ڶ���������ÿСʱ9ǧ���ٶȵ�У�����У���ѿ���6���ӣ�����������С����ʱ����ѧУ�ſڣ���ôС�������г����ٶ�Ӧ��ΪÿСʱ����ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�AB=4��BC=5����ABC=60�㣬ƽ���ı���ABCD�ĶԽ���AC��BD���ڵ�O������O��OE��AD����OE= �� 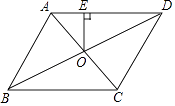
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ� С����������һ�����⣺��ͼ1���ڡ�ABC�У���D���߶�BC�ϣ���BAD=75�㣬��CAD=30�㣬AD=2��BD=2DC����AC�ij���
С�ڷ��֣�����C��CE��AB����AD���ӳ����ڵ�E��ͨ�������ACE�����������ͼ����ܹ�ʹ����õ��������ͼ 2����
��ش����ACE�Ķ�����AC�ij���
�ο�С��˼������ķ�����������⣺
��ͼ 3�����ı��� ABCD�У���BAC=90�㣬��CAD=30�㣬��ADC=75�㣬AC��BD���ڵ�E��AE=2��BE=2ED����BC�ij���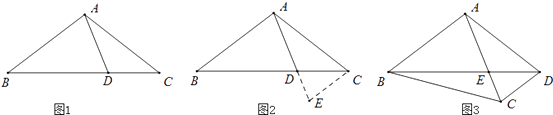
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com