
分析 (1)原式利用因式分解法求出解即可;
(2)原式利用配方法求出解即可;
(3)原式整理后,利用因式分解法求出解即可;
(4)原式整理后,开方即可求出解.
解答 解:(1)分解因式得:(x-2)(x+3)=0,
解得:x1=2,x2=-3;
(2)方程整理得:x2-4x=7,
配方得:x2-4x+4=11,即(x-2)2=11,
开方得:x-2=±$\sqrt{11}$,
解得:x1=2+$\sqrt{11}$,x2=2-$\sqrt{11}$;
(3)方程整理得:x(2x-5)-2(2x-5)=0,
分解因式得:(x-2)(2x-5)=0,
解得:x1=2,x2=2.5;
(4)方程整理得:(2x+3)2=(x-3)2,
开方得:2x+3=x-3或2x+3=3-x,
解得:x1=-6,x2=0.
点评 此题考查了解一元二次方程-因式分解法,以及配方法,熟练掌握各种解法是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
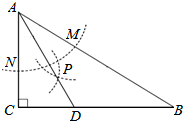 如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+1)(a-1)=a2-1 | B. | x2-4x+5=x(x-4)+5 | C. | 3x2-6x=-6x+3x2 | D. | 8a-4a2-4=-4(a-1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | 0.000001 | 0.001 | 1 | 1000 | 1000000 |
| $\root{3}{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
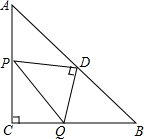 如图,等腰Rt△ABC中,∠C=90°,AC=BC,D是AB的中点,P是线段AC上的动点,连接PD,作DQ⊥PD交线段CB于Q,连接PQ,则点P从A向C方向运动过程中,△CPQ的面积变化是先逐渐增大,再逐渐减小.
如图,等腰Rt△ABC中,∠C=90°,AC=BC,D是AB的中点,P是线段AC上的动点,连接PD,作DQ⊥PD交线段CB于Q,连接PQ,则点P从A向C方向运动过程中,△CPQ的面积变化是先逐渐增大,再逐渐减小.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
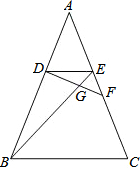 已知:如图,在△ABC中,点D、E分别是AB、AC上的点,且AD=AE,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证:
已知:如图,在△ABC中,点D、E分别是AB、AC上的点,且AD=AE,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com