
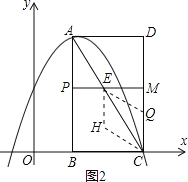
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������B��1��0����C��3��0����D��3��4������AΪ�����������y=ax2+bx+c����C������P�ӵ�A���������߶�AB���B�˶���ͬʱ����Q�ӵ�C���������߶�CD���D�˶�����P��Q���˶��ٶȾ�Ϊÿ��1����λ���˶�ʱ��Ϊt�룮����P��PE��AB��AC�ڵ�E��

��1��ֱ��д����A�����꣬����������ߵĽ���ʽ��
��2������E��EF��AD��F�����������ڵ�G����tΪ��ֵʱ����ACG�����������ֵΪ���٣�
��3���ڶ���P��Q�˶��Ĺ����У���tΪ��ֵʱ���ھ���ABCD�ڣ������߽磩���ڵ�H��ʹ��C��Q��E��HΪ������ı���Ϊ���Σ���ֱ��д��t��ֵ��
���𰸡���1��A��1��4����y=��x2+2x+3����2����t=2ʱ��S��ACG�����ֵΪ1����3��t=20��8![]() ��t=
��t=![]() ��
��
�������������������1�����ݾ��ε����ʿ���д����A�õ����ꣻ�ɶ���A���������������ߵĶ���ʽ����Ϊy=a��x-1��2+4��Ȼ��C��������룬�������ϵ��a��ֵ�����ô���ϵ�����������ߵĽ���ʽ������2�����ô���ϵ�������ֱ��AC�ķ���y=-2x+6����ͼ��������任������õ�P�����꣨1��4-t�����ݴ˿�����õ�E�������꣬�������ֱ��AC���̿�����õ�E���G�ĺ����ꣻȻ���������߷��̡�ͼ��������任�������GE=4-![]() ����A��GE�ľ���Ϊ��C��GE�ľ���Ϊ2-
����A��GE�ľ���Ϊ��C��GE�ľ���Ϊ2-![]() �������������ε������ʽ�������S��ACG=S��AEG+S��CEG=-
�������������ε������ʽ�������S��ACG=S��AEG+S��CEG=-![]() ��t-2��2+1���ɶ��κ�������ֵ���Խ��t=2ʱ��S��ACG�����ֵΪ1����3����Ϊ�������ڱ���ȵ�ƽ���ı��Σ����Ե�H��ֱ��EF�ϣ�
��t-2��2+1���ɶ��κ�������ֵ���Խ��t=2ʱ��S��ACG�����ֵΪ1����3����Ϊ�������ڱ���ȵ�ƽ���ı��Σ����Ե�H��ֱ��EF�ϣ�
���������
(1)A(1��4).
������֪�����������߽���ʽΪy=a(x1)2+4��
�������߹���C(3��0)��
��0=a(31)2+4��
��ã�a=1��
�������ߵĽ���ʽΪy=(x1)2+4,��y=x2+2x+3.
(2)��A(1��4)��C(3��0)��
�����ֱ��AC�Ľ���ʽΪy=2x+6.
�ߵ�P(1��4t).
�ཫy=4t����y=2x+6��,��õ�E�ĺ�����Ϊx=1+![]() .
.
���G�ĺ�����Ϊ1+![]() �����������ߵĽ���ʽ���������G��������Ϊ4
�����������ߵĽ���ʽ���������G��������Ϊ4![]() .
.
��GE=(4![]() )(4t)=t
)(4t)=t![]() .
.
�֡ߵ�A��GE�ľ���Ϊ![]() ,C��GE�ľ���Ϊ2
,C��GE�ľ���Ϊ2![]() ��
��
��S��ACG=S��AEG+S��CEG=![]() EG
EG![]() +
+![]() EG(2
EG(2![]() )
)
=![]() 2(t
2(t![]() )=
)=![]() (t2)2+1.
(t2)2+1.
��t=2ʱ��S��ACG�����ֵΪ1.
(3)��һ�������ͼ1��ʾ,��H��AC���Ϸ�,���ı���CQEH������֪CQ=CE=t,

������APE�ס�ABC��֪
![]() ����
����![]() �����t=20
�����t=20![]() ��
��
�ڶ��������ͼ2��ʾ��
��H��AC���·������ı���CQHE������֪CQ=QE=EH=HC=t��PE=![]() t,EM=2
t,EM=2![]() t��MQ=42t.
t��MQ=42t.
����ֱ��������EMQ��,���ݹ��ɶ���֪EM2+MQ2=EQ2,��(2![]() t)2+(42t)2=t2��
t)2+(42t)2=t2��
���,t1=![]() ,t2=4(��������,��ȥ).
,t2=4(��������,��ȥ).
��������,t=20![]() ��t=
��t=![]() .
.


 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
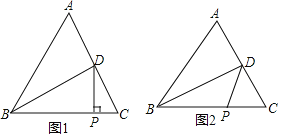
����Ŀ����֪����ͼ����ABC�У�![]() ��BDƽ�֡�ABC��BC���ж���P��
��BDƽ�֡�ABC��BC���ж���P��
��1��DP��BCʱ����ͼ1������֤��![]() ��
��
��2��DPƽ�֡�BDCʱ����ͼ2����BD��CD��CP�����к�������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������1��һ��أ�![]() ����ͬ����
����ͬ����![]() ��ˣ�
��ˣ�![]() ��Ϊ
��Ϊ![]() .��
.��![]() ����ʱ��3������2Ϊ��8�Ķ�������Ϊ
����ʱ��3������2Ϊ��8�Ķ�������Ϊ![]() ����
����![]() ��
��
��1������![]() __________��
__________��![]() __________.
__________.
����2���¹涨һ�����㷨����Ȼ��1��![]() �����˻���
�����˻���![]() ��ʾ�����磺
��ʾ�����磺![]() ��
��![]() ��
��![]() ��
��![]() ���������ֹ涨��
���������ֹ涨��
��2���������õ�ʽ��![]() ��
��![]()
��3����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��D��E�ֱ��Dz��ȱ�������ABC����AB��BC��AC���ı�AB��AC���е㣮O�ǡ�ABC����ƽ���ϵĶ��㣬����OB��OC����G��F�ֱ���OB��OC���е㣬˳�����ӵ�D��G��F��E��
��1����ͼ������O�ڡ�ABC���ڲ�ʱ����֤���ı���DGFE��ƽ���ı��Σ�
��2�����ı���DGFE�����Σ���OA��BCӦ����������������ϵ����ֱ��д���𰸣�����Ҫ˵�����ɣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڡ�ABC�У�AB��AC��AB�Ĵ�ֱƽ���߽��߶�AC��D������ABC�͡�DBC���ܳ��ֱ���60 cm��38 cm�����ABC�������͵ױ�BC�ij��ֱ���( )
A. 22cm��16cmB. 16cm��22cm
C. 20cm��16cmD. 24cm��12cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�EΪAD���ϵ�һ�㣬��C����CF��CE��AB���ӳ����ڵ�F.
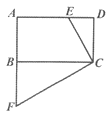
��1����֤����CDE�ס�CBF��
��2����BΪAF���е㣬CB=3��DE=1����CD�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
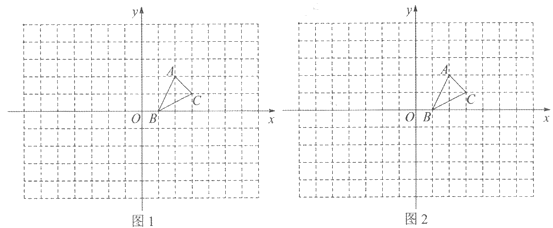
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���B������Ϊ��1��0��
��1����ͼl�л�����ABC����x��ԳƵ���A1B1C1��
��2����ͼ2�У��Ե�OΪλ�����ģ�����ABC�Ŵ�ʹ�Ŵ�����A2B2C2����ABC�Ķ�Ӧ�ߵı�Ϊ2��1������һ�ּ��ɣ�. ֱ��д����A�Ķ�Ӧ��A2������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y=ax2+4ax+4a-4��a��0���Ķ���ΪA.
��1����A�����ꣻ
��2�����㣨0��5����ƽ����x���ֱ��l����������y=ax2+4ax+4a-4��a��0������B��C����.
�ٵ�a=1ʱ�����߶�BC�ij���
�ڵ��߶�BC�ij���С��8ʱ��ֱ��д��a��ȡֵ��Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ܡ��Ĺ���ͬѧ�Ƕ��dz���Ϥ��ͼ�е��߶�OD������OABC��ʾ����������ʱ·����ʱ��Ĺ�ϵ���������ͼ�и�������Ϣ�������������.
��1����գ�����OABC��ʾ���ܹ�����_______������ӡ����ڹꡱ����·����ʱ��Ĺ�ϵ�����ܵ�ȫ������___________��.
��2�����������ÿ�����ܶ�����?�ڹ�ÿ�����������ף�
��3���ڹ����˶��ٷ�����������˯�������ӣ�
��4�����������٣���400��/�ֵ��ٶ������յ㣬������DZ��ڹ�������0.5���ӣ��������������м�ͣ��˯�����˶��ٷ���.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com