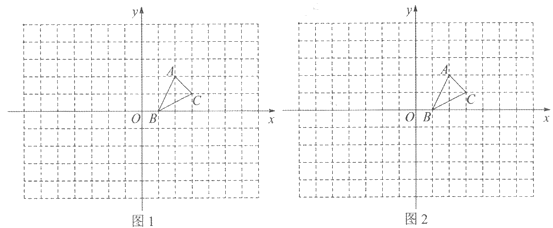
[题目]如图.方格纸中的每个小方格都是边长为1个单位的正方形.在建立平面直角坐标系后.△ABC的顶点均在格点上.点B的坐标为(1.0)(1)在图l中画出△ABC关于x轴对称的△A1B1C1,(2)在图2中.以点O为位似中心.将△ABC放大.使放大后的△A2B2C2与△ABC的对应边的比为2:1. 直接写出点A的对应点A2的坐标. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1，0）

（1）在图l中画出△ABC关于x轴对称的△A1B1C1；

（2）在图2中，以点O为位似中心，将△ABC放大，使放大后的△A2B2C2与△ABC的对应边的比为2：1（画出一种即可）. 直接写出点A的对应点A2的坐标.

【答案】（1）作图见解析；

（2）作图见解析；此时点A的对应点A2的坐标是（-4，-4）或（4，4）

【解析】试题分析：（1）分别作出点A、B、C关于x轴对称的点，然后顺次连接即可；

（2）延长OB到B2，使OB2=2OB，按同样的方法得到点A2、C2，然后顺次连接，写出A2的坐标即可.（也可以反向延长）.

试题解析：（1）如图所示;

（2）如图所示，A2的坐标是（-4，-4）或（4，4）.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，一次函数的图像与反比例函数在第一象限内的图像交于和两点．

（1）求反比例函数的表达式；

（2）在第一象限内，当一次函数的值大于反比例函数的值时，写出自变量的取值范围；

（3）求面积．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．

解：设x2－4x=y

原式=（y+2）（y+6）+4 （第一步）

= y2+8y+16 （第二步）

=（y+4）2 （第三步）

=（x2－4x+4）2 （第四步）

回答下列问题：

（1）该同学第二步到第三步运用了因式分解的_______．

A．提取公因式 B．平方差公式 C．两数和的完全平方公式 D．两数差的完全平方公式

（2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）

若不彻底，请直接写出因式分解的最后结果_________．

（3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax2+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．

（1）直接写出点A的坐标，并求出抛物线的解析式；

（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？

（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为落实“绿水青山就是金山银山”的发展理念，某县政府部门决定，招标一工程队负责完成一座水库的土方施工任务．该工程队有A，B两种型号的挖掘机，已知1台A型和2台B型挖掘机同时施工1小时共挖土80立方米，2台A型和3台B型挖掘机同时施工1小时共挖土140立方米．每台A型挖掘机一个小时的施工费用是350元，每台B型挖掘机一个小时的施工费用是200元．

（1）分别求每台A型，B型挖掘机一小时各挖土多少立方米？

（2）若A型和B型挖掘机共10台同时施工4小时，至少完成1360立方米的挖土量，且总费用不超过14000元．问施工时有哪几种调配方案？且指出哪种调配方案的施工费用最低，最低费用多少元？

查看答案和解析>>

科目：初中数学 来源： 题型：